第 6 章 清晰断点回归
本章是对清晰断点回归的极简介绍。
6.1 思路
以下是学者最开始用清晰断点回归处理的例子。假设依据GPA(x)确定授予/不授予奖学金,具体方案如下:
- GPA≥3.9,授予奖学金;
- GPA<3.9,不授予奖学金。
问题:获得奖学金会改变学习计划(y)吗?这是可能的,比如大三面临考研,如果有足够的预算,理性的选择是采取一些有效率但费钱的方式,如报考研班(假设报班是有效率的)。得到奖学金,扩大了预算,提高了报考研班的概率——奖学金改变了学习计划。
怎么估计奖学金对学习计划的影响?一个简单的想法是比较得到和未得到奖学金的同学,将他们在学习计划方面的差异认定为奖学金对学习计划的影响。这样做有问题。想想为什么有的同学总能得到奖学金。因其学习计划性本来就比较好:看手机少看书多,有计划,遵守计划等。即使没有奖学金这个事,也会观测到两类学生在学习计划方面的差异。
但可以比较GPA刚好超过临界值3.9(3.9+ε,ε为任意小的正数)一点点的同学张三和刚好低于3.9(3.9-ε)一点点的同学李四。两人GPA微小的差距很可能是偶然因素造成的,如张三的跪舔得到了回应使其考试时状态好,而李四考试时感冒了。本身来讲,两人学习计划性差距甚微。但张三就是得到了奖学金,而李四未得。是否得到奖学金这件事这可能影响到学习计划性。因此,如果发现两人在学习计划方面存在明显的差异,那么这一差异几乎就是奖学金造成的。
严格地讲,两人学习计划性的差异包含两部分:第一,本身学习计划性的差异,由基因等决定。第二,奖学金对学习计划性的影响。当ε趋近于0时,两人GPA的差异趋近于0,第一部分趋近于0,两人学习计划性的差异趋近于奖学金对学习计划性的影响。
有无获得奖学金在3.9处有一个从无到有的跳跃。将3.9称为(清晰)断点。将比较(清晰)断点两侧一点点的观测值的方法称为(清晰)断点回归。
6.2 估计
图6.1是若干同学的散点图。
横轴是GPA。纵轴是学习计划性的指标y。竖线x=3.9右边的同学得到奖学金,左边未得。
竖线以右,基于这部分散点绘制拟合曲线,它是线性、连续的,当GPA从左侧趋近于3.9时,拟合值趋近于\(y_r\),对应前例中ε趋近于0时的张三。竖线以左,基于这部分散点绘制拟合曲线,它是线性、连续的,当GPA从左侧趋近于3.9时,y趋近于\(y_l\),对应前例中ε趋近于0时的李四。在断点处,拟合值有一个跳跃,幅度为\(y_r-y_l\equiv\rho\),反映奖学金对y的影响。
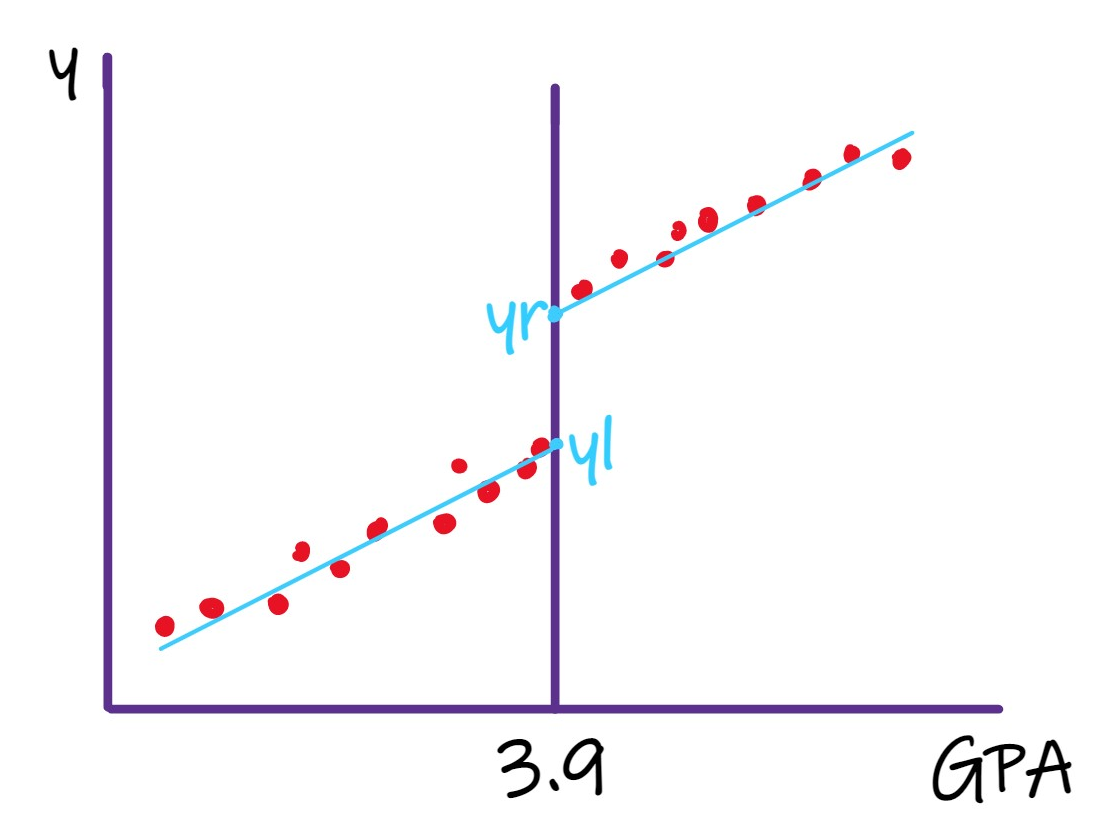
图 6.1: Sharp RDD: estimation
怎么用数学表示这个跳跃?竖线左边观测值的拟合曲线和右边观测值的拟合曲线斜率相同、截距不同。截距差就是\(y_r-y_l\),正是我们要找的奖学金对y的影响。
断点左边的拟合曲线:
\[\begin{align} \hat{\alpha}+\hat{\beta}x \tag{6.1} \end{align}\]
断点右边的拟合曲线:
\[\begin{align} \hat{\alpha}+\hat{\rho}+\hat{\beta}x \tag{6.2} \end{align}\]
涵盖所有观测值的总的拟合曲线怎么写?
如下:
\[\begin{align} \hat{\alpha}+\hat{\rho}D+\hat{\beta}x,\ D=1\ iff\ x\ge3.9 \tag{6.3} \end{align}\]
其中,D是奖学金的虚拟变量。
对应的计量模型为:
\[\begin{align} y=\alpha+\rho D+\beta x+u \tag{6.4} \end{align}\]
这是一个多元线性回归!D和x是两个自变量。D的系数表示奖学金的作用。Q:D由x构造而来,D和x之间是否存在多重共线性?
满足以下两个条件时,D的系数的OLS估计量无偏:
- x不能被操纵。在本例中,这意味着学生不能通过不正当手段左右成绩,不正当手段包括跟老师说,我GPA就差一点点就到3.9,老师您给我加2分我就可以拿奖学金了;
- 遗漏变量在断点处不存在跳跃。在例子中,这排除了下面的情况:父母宣称,子女GPA超过3.9,奖励1万元。若这样,奖学金的作用和父母奖励的作用混合在一起了,无法区分。
这两个条件比零条件均值假设弱,且可以用统计方法验证(思考验证思路)。
6.3 应用
中国冬日(城市)集中供暖以淮河为界,以北政府集中供暖,以南政府不集中供暖(见图6.2)。冬日集中供暖在人世最寒凉的时候予人温暖。同时产生空气污染物,危害人的健康,最终导致人的预期寿命减少。
如何估计冬日集中供暖对预期寿命的影响?思路是比较淮河两侧一点点的城市,淮河构成断点。数学上,只需将式(6.4)中的变量重新定义即可。定义x为城市距淮河多少纬度,在淮河以北为正,以南为负。如一个城市在淮河以北2个纬度,则其x为2;另一个城市在淮河以南1.5个纬度,则其x为-1.5。定义\(D=1\ iff\ x\ge0\)。
估计结果显示,冬日集中供暖使得预期寿命降低了约5年(Chen et al., 2013)!
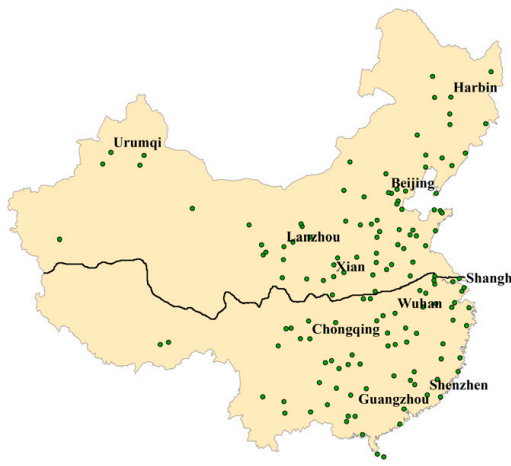
图 6.2: Map of China mainland
注:沿海诸岛略。
资料来源:Chen et al (2013)。
参考文献
- 安格里斯特, 皮施克. 基本无害的计量经济学:实证研究者指南[M]. 格致出版社, 2012, 第2.1节和6.1节.
- Chen Y, Ebenstein A, Greenstone M, et al. Evidence on the impact of sustained exposure to air pollution on life expectancy from China’s Huai River policy[J]. Proceedings of the National Academy of Sciences, 2013, 110(32): 12936-12941.