第 12 章 工具变量法:计量方法及应用
在2.6中,我们说明了对于简单回归——\(y=\alpha+\beta x\),遗漏变量和反向因果会导致:\(Cov(x,u)\neq0\),即x是内生变变量。这会导致\(\beta\)的OLS估计量:(1)是有偏的,因为\(Cov(x,u)\neq0 \Rightarrow E[u|x]\neq0\);(2)是不一致的。
怎么办?如果我们遇到的是遗漏变量问题,我们可以尝试将可能的遗漏变量加入回归。比如,在估计教育回报率的例子中,我们尝试度量IQ并加入到回归中。这是多元回归模型。有的时候,可能造成问题的遗漏因素不好测量,但如果知道它不随时间变化的话,可以通过加入个体固定效应将其纳入回归模型。这是固定效应模型。比如,在研究啤酒税对交通事故死亡率的影响时,为处理不变的酒驾社会接受度的可能影响,我们在模型中加入州固定效应。这些操作的实质是在保持这些遗漏因素不变的前提下开展研究。如不确定,请回忆多元回归和固定效应模型中系数的含义。
这一办法的局限:(1)当一个遗漏因素难以度量且随时间变化时,这一办法不适用;(2)这一办法处理不了反向因果问题。这一章要介绍的工具变量回归能克服这些局限,处理遗漏变量问题和反向因果问题。其处理问题的思路是“剥离”。
12.1 何谓“剥离”?
比如,你昨天买了一根香蕉,今早起来发现香蕉的顶部1/4变黑了,其余3/4色泽如初。你会怎么办?有钱的话,你可以把它扔了,再买一根。也有可能,你把变黑的1/4切下来扔掉,吃掉其余3/4。也就是说,你把香蕉分成两部分:变黑的1/4和其余3/4。你认为,前一部分是有问题的部分,故而切掉扔弃。经过这一剥离之后,余下3/4没有问题,可以放心食用。
另举一例,高考答卷的名字部分要密封起来。这一做法有很长的历史,至少宋代科举就这样做了,当时称作“糊名”。明代举子杨慎参加进士考试,通过糊名可以把他分成两部分:学识部分的杨慎(写出了:滚滚长江东逝水,浪花淘尽英雄…)和身份部分的杨慎(首辅大臣的儿子);剥离掉可能引起问题的身份部分的杨慎,仅以学识部分的杨慎去应试。
由此可见,剥离的思路其实我们已经非常熟悉了。
12.2 二元情形
考虑如下的简单回归模型:\(y=\beta_0+\beta_1x+u, Cov(x,u)\neq 0\)。从而x是一个内生变量。
x的分解已知
假设我们能对x做如下分解:\(x=x_1+x_2\),满足:
- \(Cov(x_1,u)=0\),即\(x_1\)与u不相关;
- \(Cov(x_2,u)≠0\),即\(x_2\)与u相关;
- \(Cov(x_1,x_2)=0\),即\(x_1\)与\(x_2\)相关。
对照上面的例子,\(x_2\)相当于香蕉变黑的1/4,是有问题的部分。\(x_1\)相当于其余3/4,是无问题的部分。参照上一节的思路,剥离有问题的\(x_2\):\(y=\beta_0+\beta_1x_1+(\beta_1x_2+u)\)。 这里,我们将\(x_2\)扔到干扰项中,\(\beta_1x_2+u\)合在一起,视之为一个新的干扰项,记为\(\epsilon\)。计量模型由此转化为:\(y=\beta_0+\beta_1x_1+ε\)。现在的问题是:在转化后的模型中,\(x_1\)和\(\epsilon\)不相关吗?
\[ Cov(x_1,\epsilon)=Cov(x_1,\beta_1x_2+u)=\beta_1Cov(x_1,x_2)+Cov(x_1,u)=0+0=0 \]
因此,在转化后的模型中,\(x_1\)是外生变量,其OLS估计量是一致的。用y对\(x_1\)回归即可得到\(\beta_1\)的一个一致估计量。
x的分解未知
以上假设可以把x分解成\(x_1+x_2\),且分解满足上述三个性质。但问题是,怎么分解?
我们需要更多的信息。假设有一变量z, 满足:
- \(Cov(z, x)\neq 0\);
- \(Cov(z, u)=0\)。
即z与x相关,但与u无关——它是一个与x相关的外生变量。
Q:基于这一信息,该如何分解?[提示:回忆2的内容]
A:用x对z进行回归:\(x=(\delta_0+\delta_1z)+\eta\)。注意,回归不要求存在因果关系(见简单回归一章)。由于\(Cov(z, x)\neq 0\),因此,\(\delta_1≠0\)。验证:\(Cov(\delta_0+\delta_1z, u)=0,Cov(\delta_0+\delta_1z,\eta)=0\)(如不清楚第二个等式缘何成立,回顾2的内容)。因此,定义:\(x_1\equiv \delta_0+\delta_1z, x_2\equiv \eta\)。这样的分解满足上述三个条件。
估计程序分为两阶段:
- 第一阶段,用x对z回归,得到\(\hat{\delta_0}\)和\(\hat{\delta_1}\),进而构建\(x_1\):\(x_1\equiv \hat{\delta_0}+\hat{\delta_1}z\),也就是拟合值;
- 第二阶段,用y对\(x_1\)回归。
经此程序,我们得到\(\beta_1\)的一个一致估计量。在每一阶段,都使用最小二乘法,用了两次,故称为两阶段最小二乘法(2SLS method)。
理解:在第一阶段,利用z,剥离掉x中内生的部分(that is problematic),仅余x外生的部分(that is problem-free)。第二阶段,用y对x外生的部分回归。z是一个剥离用的工具,称之为工具变量(Instrument variable,简称IV)。
12.3 多元情形
一般,我们遇到的情形是,模型中有多个解释变量:\(y = \beta_0 + \beta_1x + \beta_2w_1 +... + \beta_{k+1}w_k +u\)。x是核心解释变量,\(w_1,...,w_k\)是控制变量。假设\(Cov(x,u)≠0, Cov(w_1,u)=0, ..., Cov(w_k,u)=0\),即x是内生变量,控制变量是外生变量。
假设有一组变量\(z_1, ..., z_m\), 满足:
- Instrument exogeneity:\(Cov(z_i,u)=0\) for i=1, …, m,即\(z_1, ..., z_m\)是外生变量;
- Instrument relevance:在x对\(w_1, ..., w_k, z_1, ..., z_m\)的总体回归中, \(z_1, ..., z_m\)的系数不为0, 即保持\(w_1, ..., w_k\)不变, \(z_1, ..., z_m\)对预测x有帮助。
第一个性质是上一节变量z性质1的重复。第二个性质较上一节变量z性质2有所变化。回顾上一节变量z性质2:\(Cov(z, x)\neq 0 \Leftrightarrow \delta_1≠0\ (x=\delta_0+\delta_1z+\eta)\);即z对于预测x是有帮助的。这里的区别是在回归中加入了控制变量。保持\(w_1, ..., w_k\)不变,\(z_1, ..., z_m\)对预测x有帮助,用统计学的语言讲,就是说,\(z_1, ..., z_m\)与x偏相关。
称满足这两个条件的变量为工具变量。
利用这些工具变量,进行两阶段最小二乘回归:
- 第一阶段,用OLS法估计\(x=\delta_0+\delta_1w_1+...+\delta_kw_k+\delta_{k+1}z_1+...+\delta_{k+m}z_m+η\), 记拟合值为\(x_1\);
- 第二阶段,用OLS法估计\(y=\beta_0+\beta_1x_1+\beta_2w_1+...+\beta_{k+1}w_k+ε\)。
注意第一阶段中也加入了控制变量,第二阶段只是把原模型的x替换为\(x_1\)。
命题:\(\beta_1\)的2SLS估计量依概率收敛于总体参数(一致性)。
证明:仿照上一节,证明第二阶段中所有自变量都是外生变量即可。试予验证。从中可以明了为什么第一阶段需要将控制变量加入回归。
在Stata中,可以使用regress命令先后进行第一阶段和第二阶段回归。Stata也提供了一个命令自动完成这一系列过程(假设m=1,k=3):
ivregress 2sls y (x1=z1) w1 w2 w3
12.4 判断备选变量是否是合格的工具变量
以上假定满足以上两个性质的\(z_1, …, z_m\)给定。在此前提下,我们可以利用2SLS法一致地估计总体参数\(\beta_1\)。问题在于,这样的变量需要我们自己寻找。实际中的步骤是,我们提出一些备选变量,验证这些备选变量是否满足上述两个性质。若满足,它们就是合格的工具变量;反之,则须另觅变量。
假设找到一个备选变量v,下面说明如何判断此种情形下v是否满足工具变量的两个性质。
验证v满足Instrument relevance:(1)说明v与x相关的逻辑,即说明为什么你认为v应该与x相关;(2)进行统计检验,即按照这一性质的定义,估计以下回归模型:\(x=\delta_0+\delta_1w_1+...+\delta_kw_k+\delta_{k+1}v+η\)。v的系数应显著不等于0,且其符号与上述v与x相关的逻辑一致。
验证v满足Instrument exogeneity:列举原来回归(非第二阶段回归)模型中干扰项u包含的因素,要求这些因素不包含v(如包含v,意味着v直接影响因变量,自不能作为工具变量),且有理由相信这些因素与v无关(如果有理由相信某个因素与v相关,则v不是合格的工具变量)。
工具变量通常难找,因此,提出多个备选变量的情况少见,不予讨论。
具体如何做,我们通过一个例子说明,这个例子援引自斯托克和沃森(2012)第12.1.5节。
例:研究美国各州香烟的需求函数:\(Ln(Q_i)=\alpha+\beta Ln(P_i)+u_i\)。其中,i表示州,Q表示香烟销量,P表示香烟价格。该模型存在反向因果:一方面,价格影响需求量(需求函数)。另一方面,市场出清时需求量就等于供给量,供给量也会影响价格(供给函数)。存在反向因果意味着,\(Ln(P_i)\)是内生变量。需要寻找工具变量。现提出如下的备选变量:\(SalesTax_i\),表示对每包香烟征收的销售税, 由州政府设定,各州不一。
检验Instrument relevance是否成立:(1)从逻辑上讲,供给方会把部分或全部销售税转嫁给消费者,导致香烟销售税和价格正相关;(2)用\(Ln(P_i)\)对\(SalesTax_i\)回归,\(SalesTax_i\)的估计系数为0.031(标准误为0.005),显著异于0,且符号与逻辑一致。
检验Instrument exogeneity是否成立:\(u_i\)中不包含\(SalesTax_i\),即后者不直接影响价格。但\(u_i\)中包含人均收入。一般来说,人均收入越高,对健康生活方式的需求越大,对香烟的需求越小。同时,人均收入高的州政府可能更多地依靠个人所得税筹资,而非销售税筹资,故人均收入与销售税之间存在负相关。由于人均收入是u的组成部分,有理由认为u和销售税是相关的,Instrument exogeneity不成立。说明:只需要从u中找出任一个因素与销售税相关,即可否定Instrument exogeneity;而要说服他人相信Instrument exogeneity成立,则需要列出干扰项中包含的尽可能多的因素,说明这些因素与内生变量不相关的理由。
由于Instrument exogeneity不成立,\(SalesTax_i\)不是一个合格的工具变量。
这个例子透露出,寻找工具变量并不是一件容易的事。这并不是说工具变量无迹可寻。存在一些寻找工具变量的套路。接下来介绍一个常用的套路。
12.5 寻找工具变量:利用内生变量变异的外生来源
所谓内生变量变异是指不同的观测值的内生变量取不尽相同的值。为什么有的观测值的内生变量取值大,而有的观测值的内生变量取值小?有很多原因。我们尝试追踪内生变量变异的外生来源,即与未纳入模型的因变量的决定因素无关的来源。基于这样的外生来源,分离出内生变量变异中的外生部分。这样做的前提是,我们对内生变量变异的来源有充分的认知,这要求我们对相关的背景有充分的了解。以下介绍循此思路的两个范例。
Hoxby(2000)
Hoxby(2000)基于美国横截面数据,研究:Does Competition among Public Schools Benefit Students and Taxpayers?
美国业务教育阶段公立学校学额分配采取租售同权原则,即一个学区内的租户也有权上该学区的公立学校。租房的成本相对较低,因此,学生及其家庭能够以较低的成本在学区间流动,导致学区间面临着争夺生源的竞争。生源竞争的激烈程度依不同都市区而有不同。本文考虑的问题是,一个都市区内学区间的竞争能否提高效率,使得学生和纳税人受益?
计量模型如下:
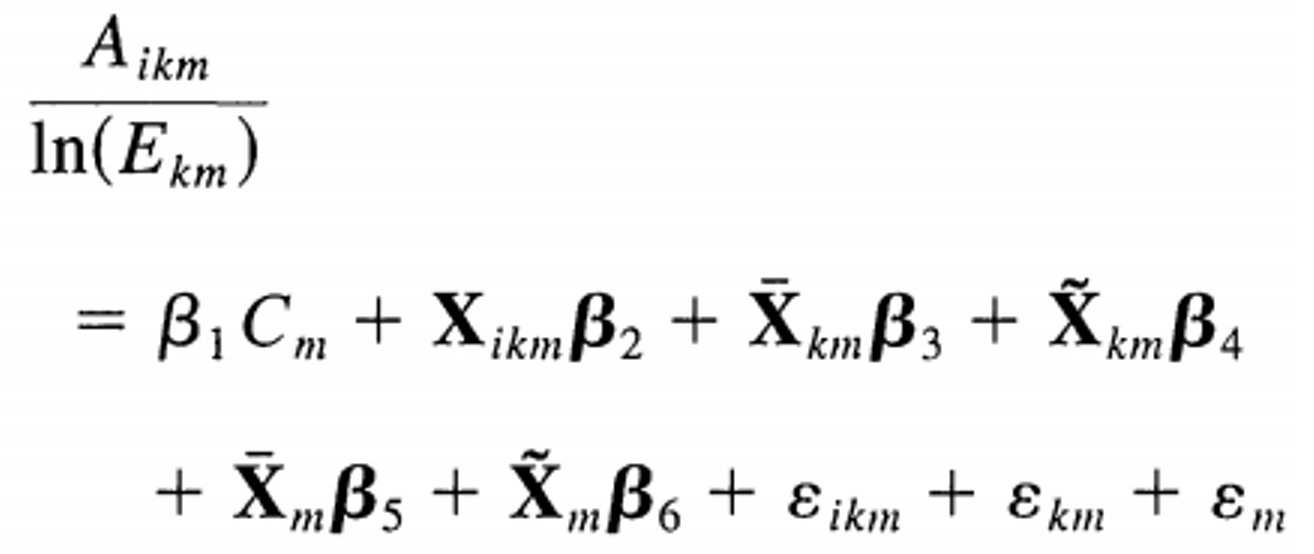
图 12.1: Econometric model in Hoxby (2000)
其中,i index individual students and their associated households. k index school districts, and let m index educational markets (i.e., metropolitan areas in this paper)。\(C_m\) measure how much Tiebout choice exists in educational market m (e.g., the number of districts per student in the metropolitan area)。简单说,它度量都市区内学区间竞争程度。最直接的一个度量指标是,生均学区数。因变量为反映公立学校绩效的指标。
由于担心可能遗漏了一些因素,这些因素与\(C_m\)相关,导致\(C_m\)为内生变量,作者使用了如下的工具变量:number of streams-that reflect the number of natural school district boundaries in a metropolitan area。作者陈述使用这一工具变量的理由如下:
Instrument relevance:
The logic is that in the eighteenth and nineteenth centuries, when school district boundaries were initially set in America, an important consideration was students’ travel time to school. Natural barriers could significantly increase travel time. With automobiles, buses, paved roads, bridges, and flood controls, many of the barriers that would have caused students to travel miles out of their way are now hardly noticed. Yet, the vestigial importance of natural barriers is preserved because they determined initial school-district boundaries, which are the key supply-side factor that determines today’s boundaries. Thus, the number of school districts in a given land area at a given time of settlement was an increasing function of the number of natural barriers. I focus on streams, because they are the most common and most easily quantified natural barriers.
文中这一段阐述了streams影响学区划分的逻辑。作者继续进行了第一阶段回归:因变量为\(C_m\),自变量为number of larger streams in metropolitan area、number of smaller streams in metropolitan area和控制变量。结果显示,number of larger streams in metropolitan area和number of smaller streams in metropolitan area的系数均显著为正(见文中表2),与所述逻辑一致。
Instrument exogeneity:
What about the second condition for valid instrumental variables-that streams are exogenous to school productivity? The condition is highly plausible.
对此作者未给出明确的解释。我们尝试把外生性的逻辑补全。首先,number of streams不会直接影响到公立学校的绩效如学生成绩,这一点当是合理的。然后,得说明number of streams跟其他影响学生成绩的指标不相关。想一想,有的同学家住在南京市区,从家驱车来校,途中你不会注意经过了多少条溪流?除非你喜欢钓鱼。也就是说,在你的观念里,溪流不会影响到我们的学习、工作以及商业活动等——溪流跟学习、工作以及商业活动不相关。既如此,它跟学生成绩也应不相关。
第二阶段回归的结果表明,学区间竞争越大,公立学校学生12年级阅读分数越高(见文中表3),per-pupil spending越小,share of students in private school越小(见文中表5),12年级阅读分数与log(per-pupil spending)的比值越大(见文中表7)。因此,学区间竞争提高了公立学校的效率。
在这篇文章中,学区间竞争程度的变异有很多来源。作者基于对学区制度的了解,追踪到地理信息这一学区间竞争程度变异的外生来源。基于这一外生来源分离学区间竞争程度的外生部分,从而识别其对公立学校绩效的因果影响。
Acemoglu et al.(2001)
11.5提供了人力资本积累促进经济增长的经验证据。Acemoglu et al.(2001)则研究制度对经济发展的影响。
其计量模型如下:
\[ logy_i=\mu+\alpha R_i+X_i^{'}\gamma+\epsilon_i \] 符号的含义:
- i指国家;
- \(y_i\)是人均收入指标,具体指log GDP per capita in 1995或log output per worker in 1988;
- \(R_i\) is the protection against expropriation measure,具体指average protection against expropriation risk during 1985-1995,即产权保护程度指标,反映制度水平;
- \(X_i\) is a vector of other covariates;
- \(\epsilon_i\) is a random error term.
作者关注前被殖民的国家。这些国家的制度水平\(R_i\)可能是内生变量。作者用工具变量法处理内生性。国家制度水平由很多因素决定,作者尝试从历史中寻找制度水平差异的外生来源。作者提出使用如下的工具变量: Log European Mortality Settler,即19世纪初在殖民地定居的欧洲殖民者的死亡率的对数。
验证Instrument relevance:(1)逻辑上,“Europeans adopted very different colonization policies in different colonies, with different associated institutions. In places where Europeans faced high mortality rates, they could not settle and were more likely to set up extractive institutions. These institutions persisted to the present”;(2)如图12.2的Panel B所示,第一阶段回归的结果显示,此变量显著为负,与上述逻辑一致。
验证Instrument exogeneity:由于医疗卫生条件的飞速进步,两百年前致死的疟疾、黄热等病菌现在已不足为患,不会影响今日的经济绩效。
第二阶段回归的结果见图12.2的Panel A。前8列的因变量为log GDP per capita in 1995。第9列的因变量为log output per worker in 1988。在各列中,average protection against expropriation risk during 1985-1995的系数均显著为正,表明良好的产权保护促进了经济发展。
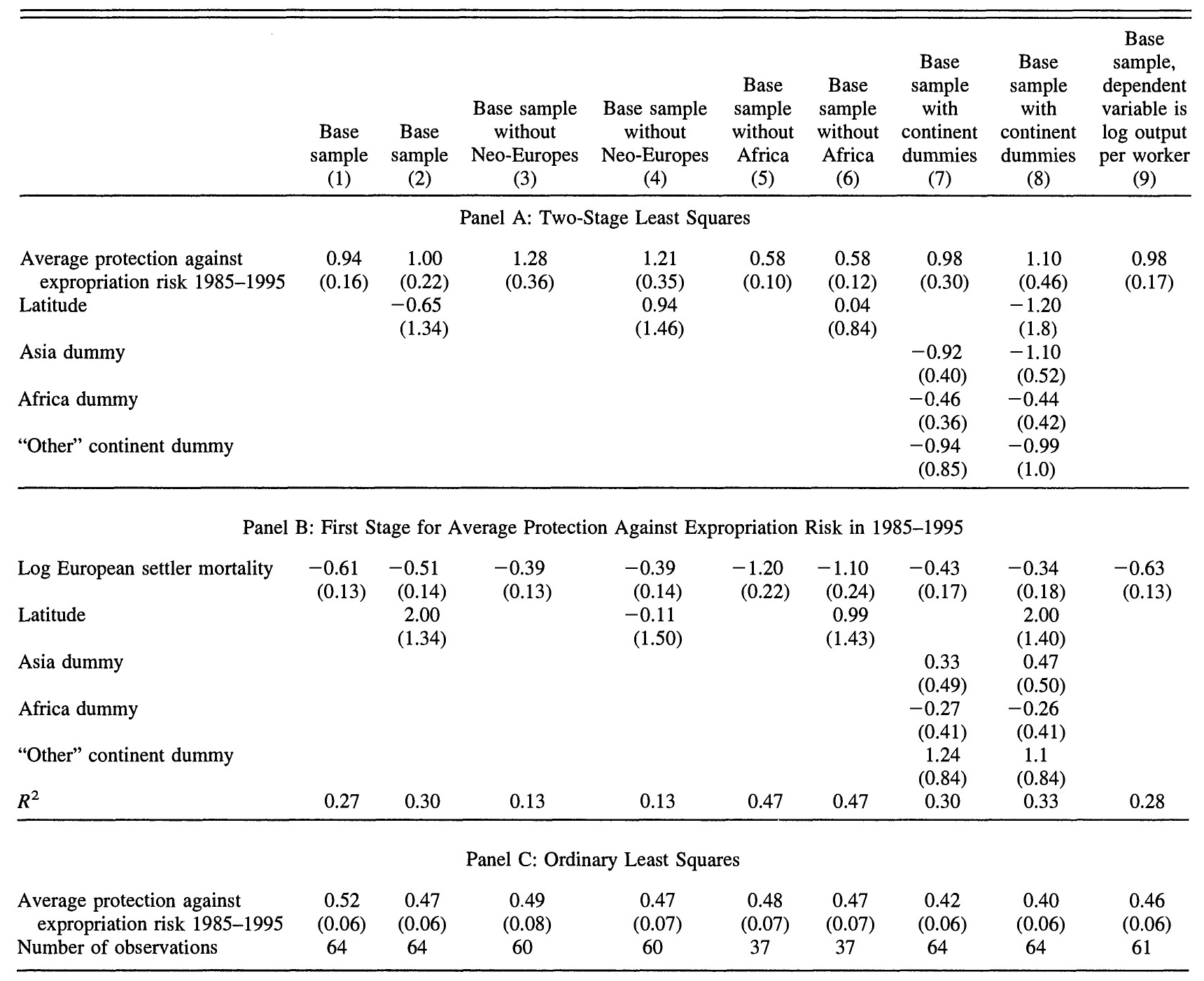
图 12.2: Effect of institutions on economic performance
资料来源:Acemoglu et al.(2001)表4。
斯托克和沃森(2012)第12章对工具变量有更为详尽的介绍,包括工具变量法的发明,请自行阅读。
参考文献
- 斯托克, 沃森. 计量经济学导论(第三版)[M]. 中国人民大学出版社, 2014, 第12章.
- Acemoglu D, Johnson S, Robinson J A. The colonial origins of comparative development: An empirical investigation[J]. American economic review, 2001, 91(5): 1369-1401.
- Hoxby C M. Does competition among public schools benefit students and taxpayers?[J]. American Economic Review, 2000, 90(5): 1209-1238.