第 11 章 基于面板数据的双重差分法:计量方法及应用
考虑一个扶贫项目:某县教育局定点扶贫县内一个贫困村,为期五年。五年间该村收入增长了30%,宣告脱贫。
Q:该村五年间收入增长30%是否由该扶贫项目导致?如果否,怎么估计该扶贫项目的收入增长效应?
11.1 双重差分法的思路
根据安格里斯特和皮施克(2012,第5.2节),双重差分法的用可以追溯至一百多年前。本节以下是对该书该节的转述和解读。
19世纪中期,伦敦霍乱问题严重。当时流行的观点是,霍乱通过糟糕的空气传播。
John snow(1855)提出一个新的观点:霍乱通过受污染的水传播。他观察到如下事实。 1849年,有一个叫Lambeth的水厂从伦敦中部河流下游水质差的Thames地区汲水,处理后供给伦敦的一部分家庭。1852年,它将水厂迁址到该河流上游水质好的一个地方。尽管水厂搬了,它的供水区不变。搬厂后其供水区霍乱致死数大幅减少。Q:1949-1852年Lambeth供水区霍乱致死数的减少是不是全由供水质量改善导致?
三年间Lambeth供水区霍乱致死数的减少(总效应)包含了两种效应。其一,水质改善的效应(净效应)。其二,这段时间医疗卫生条件改善的效应。例如,研发出一种对霍乱有效的新药。全国都可以用这个药,因此,包括Lambeth的供水区在内的全国各地的霍乱致死数都会减少。称这一全国各地霍乱致死数统一的减少为趋势性变化(减少)。由于我们只关心供水质量改善带来的霍乱致死数的变化,需要剔除霍乱致死数的趋势性变化。如何做?
John Snow同时观测到另一个名为S & V的水厂,1849-1952年间始终从Thames地区汲水,处理后供给家庭使用。知悉S & V供水区1849和1952年的霍乱致死数。
S & V始终没有迁址,其供水区霍乱致死数在1849-1852年间的变化反映了医疗卫生条件变化带来的趋势性变化。用其作为医疗卫生条件导致的趋势性变化的估计。这种趋势性变化对所有地区都是一样的。用Lambeth供水区霍乱致死数在1849-1852年间的变化减去S & V供水区霍乱致死数在1849-1852年间的变化,就得到供水质量的改善的净效应。这里做了两次差分。第一次差分,对Lambeth和S & V的供水区,分别用一个1852年的霍乱致死数减去1849的霍乱致死数。第二个差分,用前面一个差分减去后面一个差分。故名双重差分法。
双重差分法的关键假设是: Lambeth供水区和S & V供水区由医疗卫生条件改善导致的霍乱致死数的减少相同,即趋势性变化相同。该假设成立是该方法有效的前提。
John Snow在一百多年前使用双重差分法时计量经济学尚未诞生。如今,我们学习了计量经济学,希望在基础上更进一步,将之转化为计量模型,进而估计参数,并做统计推断。
11.2 政策一次性实施
怎么按以上思路构建计量模型?我们用一个例子说明。
中国自改革开放后,经济飞速发展。发展的代价是环境急速恶化,至20世纪90年代末,中国多个城市跻身世界空气污染最严重的城市。为改善空气质量,1998年国务院实施两控区政策,两控区指二氧化硫控制区和酸雨控制区。酸雨也是二氧化硫引起的,故此政策意在控制二氧化硫排放。两控区的范围见图11.1中灰色区域。在两控区内实施严格的环境规制,比如限制火电厂建设,要求煤脱硫后方可使用。图11.1中白色区域为非两控区,不做任何干预。两控区自然地成为处理组,非两控区成为对照组。
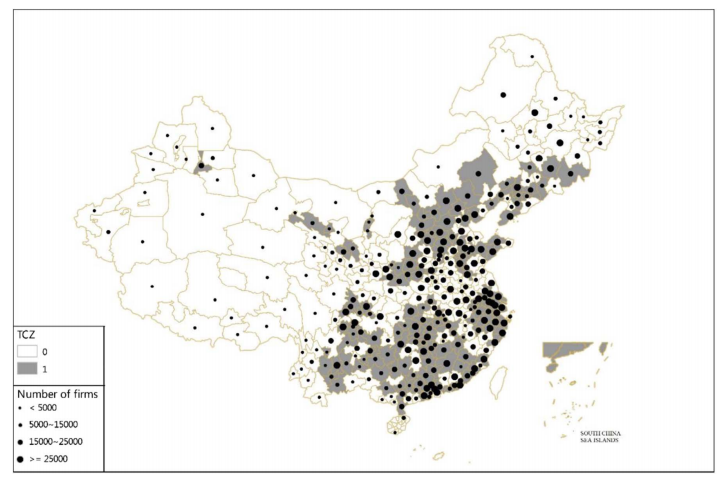
图 11.1: Locations of two control zones
资料来源:Cai et al.(2016)图1。
Tanaka(2015)研究两控区政策对婴儿死亡率的影响。预期两控区因为严格的环境管制,二氧化硫排放减少,空气质量改善,人们的健康状况改善。在人群中,婴儿对空气质量最为敏感。如空气质量不好,他们受害最大。反之,二氧化硫排放减少,空气质量改善,他们的健康改善也最明显。因此,预测随着两控区政策的实施,婴儿死亡率——这一集中反映婴儿健康状况的指标——会降低。
类前,我们不能简单地计算两控区在政策实施后的婴儿死亡率与政策实施前婴儿死亡率的差值,作为两控区政策效果的估计。这一差值一部分反映该政策的效果,另外还反映其他因素变化的作用如护理技术提高的作用。更好的护理技术,能降低婴儿死亡率。并且,护理技术在全国的传播是不需要太大成本,即如果一个新的护理技术出来,被证明行之有效,会很快在全国范围内推广,导致全国各地区婴儿死亡率降低。此所谓(对所有地区相同的)趋势性变化。
具体来分析两控区(TCZ)和非两控区(non-TCZ)在该政策实施前后的四种情况。考虑两控区城市i,将其在1995年的婴儿死亡率分解成两部分,一部分是由1995年的护理技术决定的婴儿死亡率,记为\(\lambda_{1995}\)。该记号只有一个时间下标(1995),而无城市下标,因为我们假设护理技术可以在全国迅速推广,从而在同一年对所有地方都是一样的。另一部分是城市i自身的地形决定的婴儿死亡率。想想一个以山地为主的城市,农村居民到城区或县区耗时久,孕妇不知道生产的确切时间,及至临盆,很可能就近至乡镇医院生产。乡镇医院的医疗条件通常要差一些,婴儿死亡率也就高一些。这部分婴儿死亡率用\(\alpha_i\)表示。该记号只有城市下标,没有年份下标。这意味着,它在不同地方是不一样的,但对同一个地方,由于地形长期不变,由其决定的婴儿死亡率也就不变。
来看两控区城市i在2000年的情况。此时,该政策在该城市已经实施两年了。故该城市此时的婴儿死亡率包含三项。第一项是我们关心的政策效果,用\(\rho\)表示,预期它小于0,即两控区政策改善了空气质量,从而降低了婴儿死亡率。第二项是提高后的护理技术决定的婴儿死亡率,记为\(\lambda_{2000}\)。第三项是地形决定的婴儿死亡率,由于地形在五年内保持不变,这一项也保持不变,还是\(\alpha_i\)。如果我们简单地用2000年的取值减去1995年的取值,得到:\(\rho+(\lambda_{2000}-\lambda_{1995})\);这一差值包括政策效应\(\rho\)和趋势性变化\(\lambda_{2000}-\lambda_{1995}\)。
再来看非两控区城市j。其在1995年的婴儿死亡率可以分解成两项,一项是由1995年的护理技术决定的婴儿死亡率\(\lambda_{1995}\)。注意这一项与两控区城市i当年的取值是一样的。另一部分是由该城市的地形决定的婴儿死亡率\(\alpha_j\)。等到2000年,其婴儿死亡率为\(\lambda_{2000}+\alpha_j\)。非两控区内并无相应环境规制,所以没有政策效果这一项。用非两控区城市j在2000年的取值减去其在1995年的取值,得到趋势性变化:\(\lambda_{2000}-\lambda_{1995}\)。
用以上两控区城市i在政策实施前后婴儿死亡率的差值减去非两控区城市j在政策实施前后婴儿死亡率的差值就得到政策效果\(\rho\)。如图11.2所示。
这是一种理解。
还可以从另一个角度理解。刚才横着相减做第一次差分,也可以竖着相减做第一次差分。对1995年,用两控区的婴儿死亡率减去非两控区的婴儿死亡率,得到\(\alpha_i-\alpha_i\)。\(\lambda_{1995}\)消掉了,因为护理技术在同一年之于全国各地是相同的。对2000年,重复这一操作,得到\(\rho+\alpha_i-\alpha_i\)。再用后一个差分减去前一个差分,同样得到了政策效果\(\rho\)。殊途同归,但该操作过程有不同的含义。1995年差分反映的是处理组和对照组之间的差异,由不同的地形所致。地形短期内保持不变,故我们将这一组间差异称为组间固有差异。2000年差分依然包括组间固有差异项,除此以外,还包括政策效果项。后者拉大或缩小了组间差异,这就是对政策效果的另一种理解。
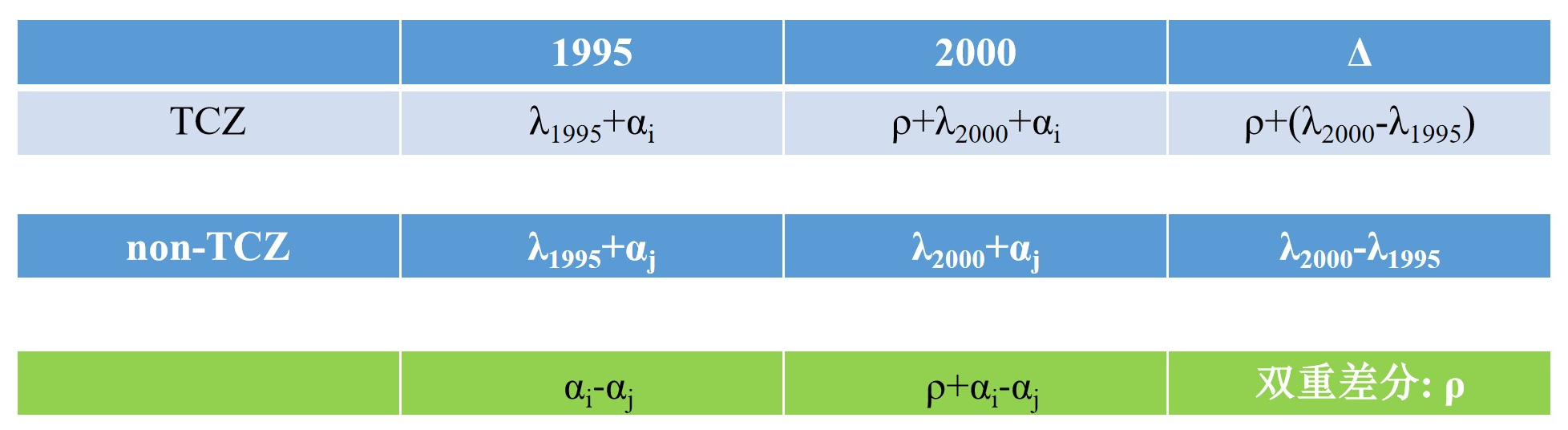
图 11.2: Infant mortality rate in four cases
将以上结果直观展示于图11.3。图中横轴表示年份,纵轴表示婴儿死亡率。如图所示,1995-2000年间,非两控区的婴儿死亡率降低(暂假设如此)。两控区的婴儿死亡率也在降低,但降得更多。假想没有实施两控区政策,两控区婴儿死亡率的变化仅由护理技术提高驱动,由于护理技术之于全国各地相同,因此其导致的全国各地婴儿死亡率的变化幅度相同,即两控区婴儿死亡率的轨迹应与非两控区婴儿死亡率的轨迹平行,如图中虚线所示。其与反映两控区婴儿死亡率真实变化的轨迹在2000年尚有差距,这一差距(多出来的降幅)即为政策效果,如图中2000年的垂线段。换一个角度,1995年两控区与非两控区之间的差异为组间固有差异(假设1995年两控区的婴儿死亡率更高)。2000年,组间差异反向了。组间差异的变化等于图中2000年的垂线段,反映政策效果。
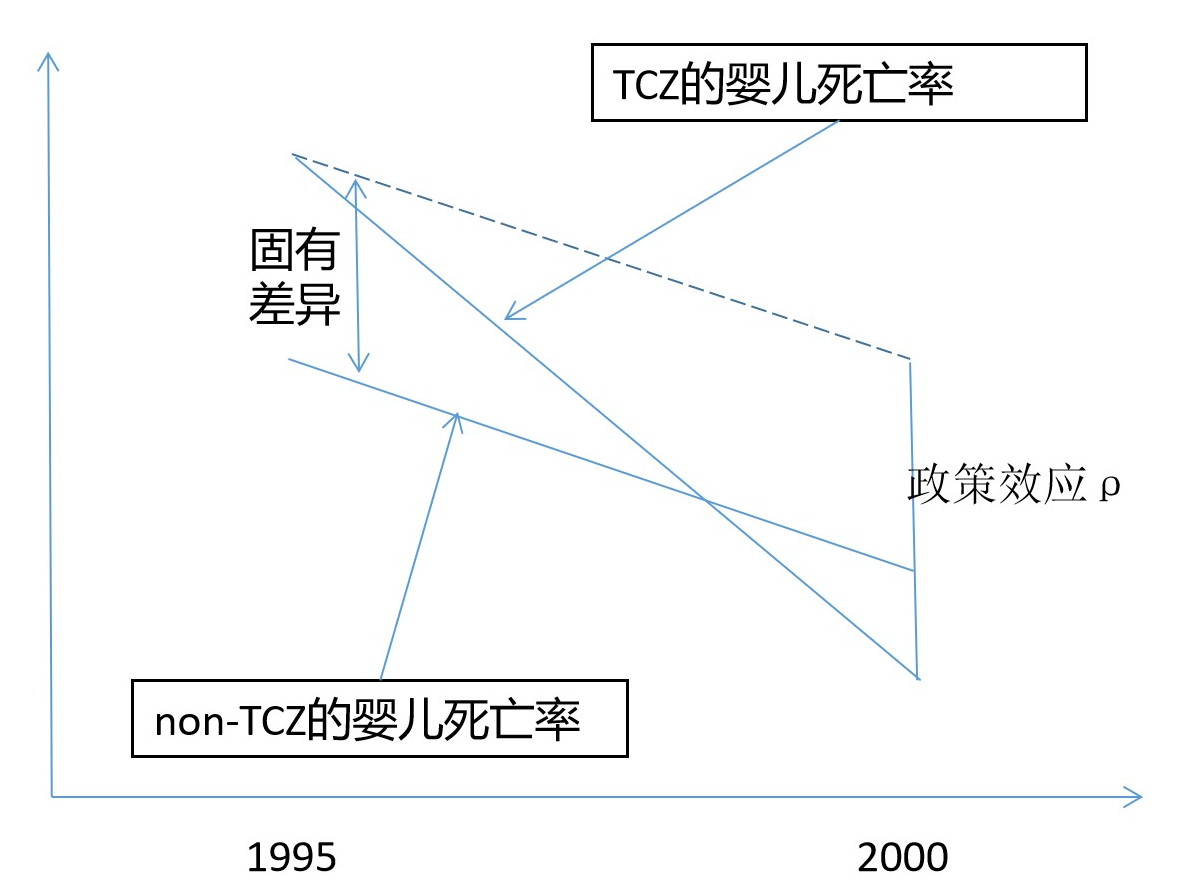
图 11.3: Illustration of infant mortality rate
接下来,我们尝试将上述思路转化为计量模型。
思考:怎么用一个统一的式子表达图11.2中的4种情况?
答案:\(\rho D_{k,t}+\lambda_t+\alpha_k\)。其中,k表示城市,t表示年份。\(D_{k,t}\)表示两控区政策的虚拟变量。赋值如下:某城市于某年实施了政策,记为1;否则,记为0。注意,取值为1的情形:是两控区城市,且在1998年政策实施后。不妨将之写为:\(\rho D_{i,t}+\lambda_t+\alpha_i\)。
以上只考虑了两年,考虑更多的年份:1995-2000年。\(D_{i,t}\)赋值如图11.4:

图 11.4: Values of policy dummy from 1995 to 2000
在上式中加入干扰项就得到一个计量模型:
\[\begin{align} y_{i,t}=\rho D_{i,t}+\lambda_t+\alpha_i+u_{i,t} \tag{11.1} \end{align}\]
其中,因变量\(y_{i,t}\)表示婴儿死亡率。这不就是一个固定效应模型吗?核心解释变量较为特殊,是一个虚拟变量。其系数表示政策效应。\(\lambda_t\)是时间固定效应,一般地,反映随时间变化、但不随个体变化的因素的作用,这些因素包括但不必局限于护理技术决定的婴儿死亡率。\(\alpha_i\)是个体固定效应,一般地,反映随个体变化、但不随时间变化的因素的作用,这些因素包括但不必局限于地形。\(u_{i,t}\)表示其他没有纳入模型的因素的作用。因此,双重差分法其实是固定效应模型的一个特例。
可以分解政策变量:\(D_{i,t}=TCZ_iPost_t\)。\(TCZ_i\)和\(Post_t\)分别是两控区城市的虚拟变量(两控区城市取1,非两控区城市取0)和政策实施后年份的虚拟变量(1998年及以后年份取1,1998年以前年份取0)。
练习:仿照图11.4,填写\(TCZ_i\)和\(Post_t\)的取值,验证:\(D_{i,t}=TCZ_iPost_t\)。
影响婴儿死亡率的因素尚有其他,如产妇年龄,大龄产妇生育相对困难。将此类可度量的因素(记为\(X_{i,t}\))纳入计量模型能缓解遗漏变量问题。
\[\begin{align} y_{i,t}=\rho D_{i,t}+\delta X_{i,t}+\lambda_t+\alpha_i+u_{i,t} \tag{11.2} \end{align}\]
或者写为:
\[\begin{align} y_{i,t}=\rho TCZ_iPost_t+\delta X_{i,t}+\lambda_t+\alpha_i+u_{i,t} \tag{11.3} \end{align}\]
这便是双重差分法的完整计量模型了。在Stata中估计(11.3),就用固定效应模型的命令:
xtreg y c.TCZ#c.Post X i.year, fe
Tanaka(2015)一文中的计量模型写作:\(y_{j,t} = \alpha+ \pi_1 T_jPost_t + \delta_1X_{j,t} + \kappa_t + \mu_j + \epsilon_{j,t}\)。注意,其中\(\alpha\)是多余的,因为可以把它加到个体固定效应中。该公式其余部分与式(11.3)只是记号变了,无实质区别。
估计结果(含稳健性检验)
回归的结果见图11.5。第一列是变量名。因变量为婴儿死亡率,单位为千分之一。\(TCZ\times Post\)是我们关心的解释变量。Observations是观测值数。其余各列一列表示一个回归。 列(1)只纳入了时间固定效应和个体固定效应(Year fixed effects和District fixed effect为Y)。\(TCZ\times Post\)的系数均显著为负。估计系数为-2.870,在5%的水平显著(如表下注,两颗星表示在5%的水平显著)。该估计值的经济学含义:两控区政策的实施使得两控区城市婴儿死亡率降低0.2870%。称这一结果为基准结果。列(2)在此基础上加入了家庭层面的控制变量,包括share of male, birth shares in respective month, birth order, mother’s age, mother with high school degree or more, Han(表中HH controls为Y)。列(3)继续加入了城市层面的控制变量,包括number of births, total population, rainfall(表中District controls为Y)。注意,表中未报告这些控制变量的估计系数,因为我们不关心。加入这些控制变量以后,\(TCZ\times Post\)的系数依然显著为负。并且,值变化不大。我们称(基准)结果对加入这些控制变量保持稳健(符号、显著性、大小保持稳定)。这是稳健性检验的一种方法,后面我们还会介绍其他稳健性检验方法。
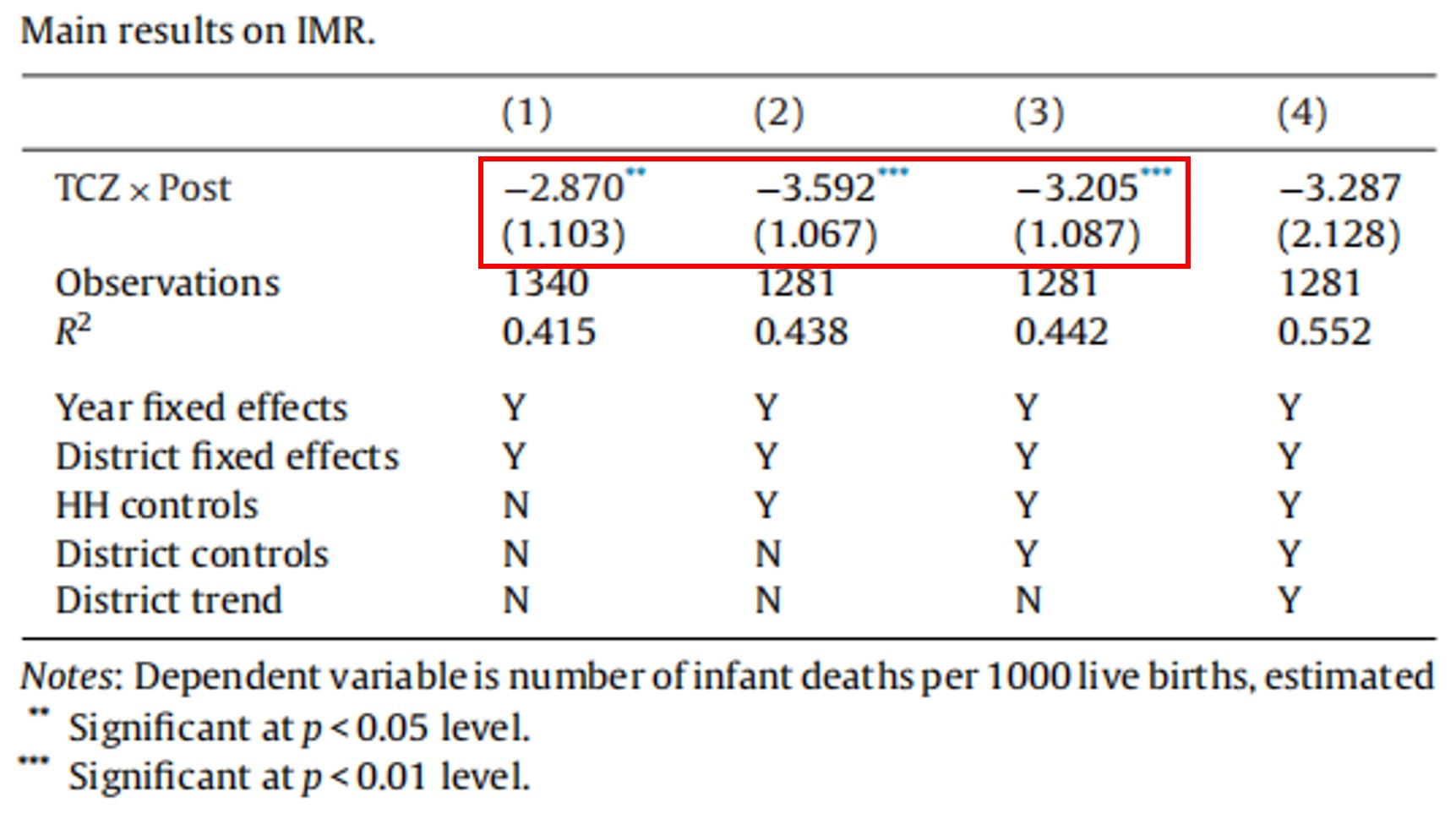
图 11.5: Effect of the TCZpolicy on IMR
资料来源:Tanaka(2015)表3。
共同趋势检验
图11.2隐含地假设两控区城市和非两控区城市具有共同时间趋势(common trend),如在1995年,两者的趋势项均为\(\lambda_{1995}\)。如果两者不具有共同时间趋势,如非两控区城市j在1995和2000年的趋势项变为\(\lambda_{1995}^{’}\)和\(\lambda_{2000}^{’}\)。双重差分法不能无偏地估计政策效应(练习:在此情形下,更新图11.2中的表格,验证这一论断)。因此,共同趋势假设成立是双重差分法有效的前提。须验证这一假设是否成立。
在图11.2和11.3中,只有1995和2000两年。引入1993年。练习:补充图11.2中1993的年取值,据此更新11.3。
可以得到,在更新后的图中,两控区婴儿死亡率在1993-1995年间轨迹与非两控区婴儿死亡率在1993-1995年间轨迹平行。背后的原因是,由于两控区城市和非两控区城市具有共同时间趋势,计算组间差异时,趋势项消掉了,组间差异在政策实施前保持不变。反之,如果共同时间趋势假设不成立,即使政策实施前,组间差异在不同的时间也不同,处理组和对照组因变量的轨迹不再平行。因此,验证共同趋势假设的一个方法是:观察两控区城市和非两控区城市的婴儿死亡率的轨迹在政策实施前是否平行。
图11.6绘制了1991-2000年两控区城市和非两控区城市婴儿死亡率的轨迹。蓝线是两控区,每一年有一个点,表示当年两控区城市婴儿死亡率的平均值。红线是非两控区。从趋势上来看,期间两控区和非两控区城市婴儿死亡率是下降的。竖线以左是政策实施前。可以看到,排除1994年,两控区城市和非两控区城市的婴儿死亡率的轨迹大致是平行的,大致可以认为具有共同时间趋势。但是,1994年,很可能没有共同时间趋势。所以,如果只使用1995-2000年的数据,估计结果可能更有说服力。
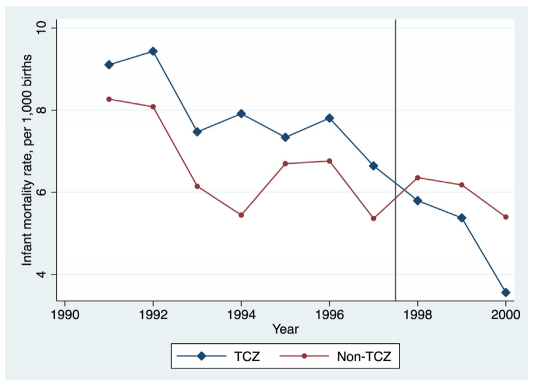
图 11.6: IMR of the treatment and control groups
资料来源:Tanaka(2015)图2。
这一检验方法基于图形,也可利用计量方法检验共同趋势假设,见附录1。
双重差分法的估计量无偏吗?
命题:如果共同时间趋势假设成立,那么,政策虚拟变量的系数的最小二乘估计量是无偏的。
从直觉上很好理解。已如上述,如果存在共同时间趋势,经过两次差分,能把趋势性变化剔除掉,得到政策效应。
数学证明见附录2。结论:如果存在共同时间趋势,政策虚拟变量的系数的最小二乘估计量是无偏的,在平均意义上能反映因果关系。
11.3 政策分多轮推进
两控区政策是一次性在全国部分地区(两控区城市)实施的。有的时候,政策分多轮推进。2003年以来推行的财政省直管县改革(PMC reform)就是这样的例子。所谓财政省直管县改革是指,改变之前省管市、市管县的财政体制,变为省直接管理市和县的财政体制。财政省直管县改革分多轮推进。例如,2004年,湖北在大部分县进行财政省直管县改革;2007年,江苏在全省辖县进行了财政省直管县改革;而有的县至今未实施该改革。
仍可使用上一节的计量模型:\(y_{i,t}=\rho D_{i,t}+\delta X_{i,t}+\lambda_t+\alpha_i+u_{i,t}\)。\(D_{i,t}\)的含义不变(i县t年实施了改革则记为1, 否则记为0)。赋值调整如下:

图 11.7: Values of policy dummy for the PMC reform
Li et al.(2016)研究财政省直管县改革对经济发展的影响。思考:预期前者影响后者的方向及理由。
作者检验了共同趋势假设。由于财政省直管县改革分多批推进,不能照搬上一节的检验方法。作者将样本期间(1995-2012年)所有实施了财政省直管县改革的县称为省直管县(不论在何时实施该改革,记其为PMC counties),在样本期间未实施该改革的县称为非省直管县(记为non-PMC counties)。计算各年两类县人均GDP的对数的均值,绘图11.8。由图可见,在2003年以前(省直管县改革尚未启动),省直管县(蓝色)和非省直管县(绿色)几乎平行,可以认为共同趋势假设成立。
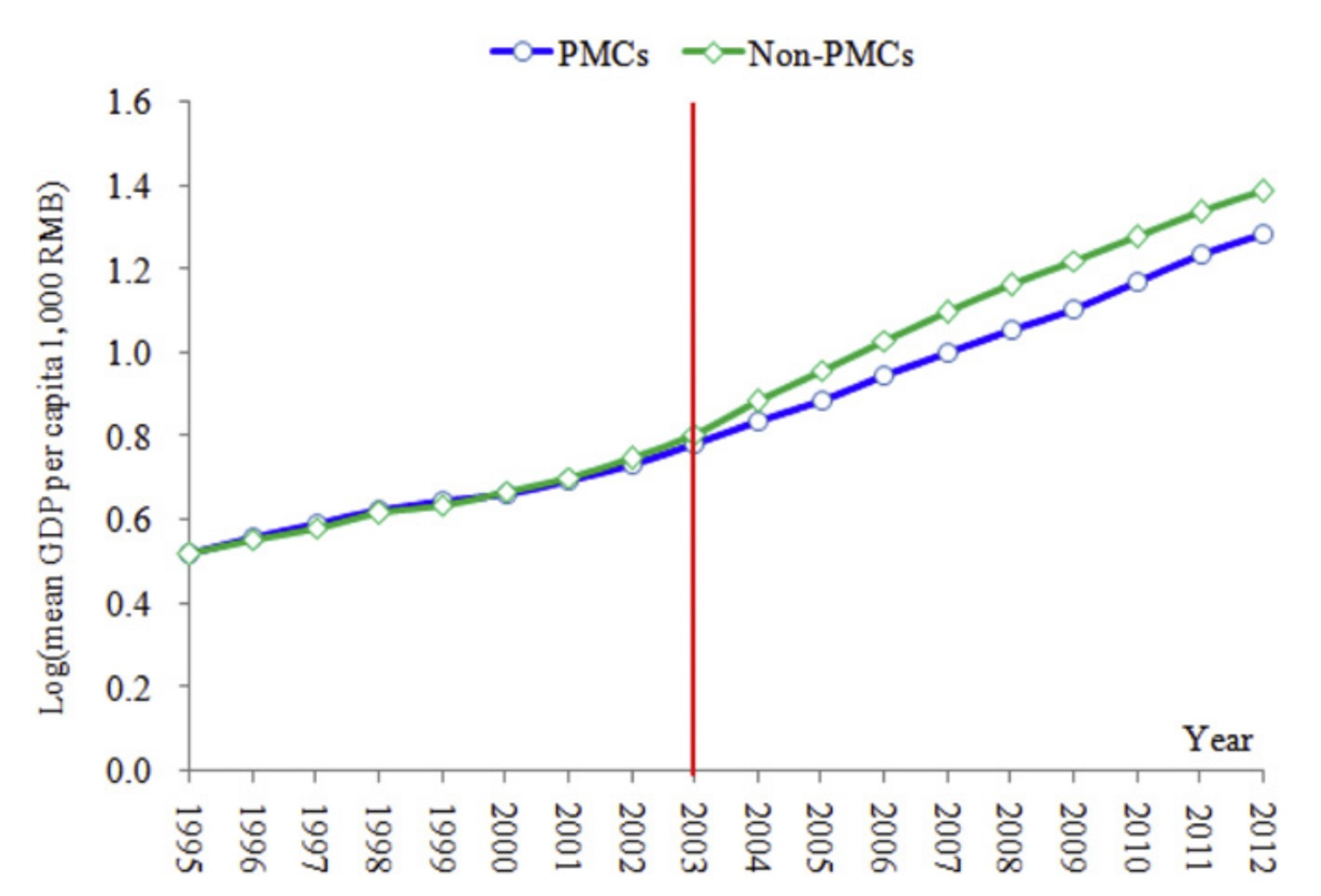
图 11.8: Common trend assuption test for the PMC reform
资料来源:Li et al.(2016)图3。
文中表3列(1)-(4)的估计结果显示,财政省直管县改革对人均GDP的对数的影响显著为负。该表列(7)将因变量替换为人均夜晚灯光亮度的对数。夜晚灯光亮度是从卫星上观测的。一般来说,一地经济越发达,卫星观测到该地夜晚灯光越亮。因此,夜晚灯光亮度被广泛用作经济发展的一个度量指标。结果显示,政策虚拟变量的系数依然显著为负。说明结果具有稳健性。更换因变量为替代指标,是另一种常见的稳健性检验方法。请自学。
想想为什么财政省直管县改革抑制了经济发展?作者在表8中进行了机制分析,方法同似7.1介绍的方法。请自行阅读。
11.4 外生事件
在以上两列中,我们用双重差分法估计政策的影响。双重差分法还可用于估计事件的影响。一般,我们关注外生事件。所谓外生事件,从数学上讲,是指度量该事件的指标与干扰项不相关。直观上,外生事件应满足:偶发,不受所研究的个人、企业或地区控制。比如,张三升任财政部部长对其来源地(如出生的城市)来说就是一个外生事件——城市难以干预中央的人事任免,张三高就对其来源地来说就如中了彩票一样。所谓一人飞升,仙及鸡犬,出任财政部部长的张三是否给其来源地带来更多的转移支付?范子英和李欣(2014)就此进行了研究。定义中央部委部长来源地虚拟变量:某中央部委部长任期内,其来源地赋值为1;否则,赋值为0。使用以上介绍的计量模型即可估计部长给其来源地带来的转移支付增量。详情请阅读此文。
11.5 基于处理强度的双重差分法
以上政策和事件,要么是有,要么是没有。是有与无的差异,或1与0的差异。有的时候,差异并非如此截然二分。1999年,中国大学开启了扩招。大学扩招促进了人力资本的积累,有利于提高各行业的生产率。也就是说,各行业都因此受益。但是,不同行业受益程度并不一致。想想大学扩招对富士康促进作用更大,还是对华为促进作用更大?应该是后者。华为需要招大量大学生,而富士康对大学生的需求不大。一般地,不同行业对人力资本的需求量是不一样的。一个行业如果对人力资本的需求大,那么它因大学扩招获益大。这里就不再是0和1的差异,而是均受益、但受益程度不一的差异,受益程度可由人力资本密集度反映,人力资本密集度可以取0.05、0.3等,故可以说是0.05、0.3等的差异。可以比较人力资本密集度高的城市(看作处理组)和人力资本密集度低的城市(看作对照组)在大学扩招前后的表现,这是双重差分法的变形,称作“基于处理强度的双重差分法”。
Che and Zhang(2018)研究大学扩招这一外生事件导致的人力资本积累对企业全要素生产率(TFP)的影响。其计量模型如下:
\[\begin{align} y_{ijt}=\alpha_i+\gamma_t+\beta\times(IndustryHC_j\times post_t)+\phi\times X_{ijt}+\epsilon_{ijt} \tag{11.4} \end{align}\]
其中,i表示企业,j表示行业,t表示年份。\(y_{ijt}\)是属于行业j的企业i在年t的TFP。\(\alpha_i\)是企业固定效应。注意,控制了企业固定效应之后就不需要控制行业固定效应了,因为行业内的企业固定效应合在一起就是行业固定效应。\(\gamma_t\)是年份固定效应。\(IndustryHC_j\) is the human capital (HC) intensity of industry j, measured by the percentage of workers with a four-year college education or more in industry j in the US in 1980。\(post_t\)是2003年及以后年份的虚拟变量。1999年大学扩招的大学生首次进入劳动力市场是2003年。因此,大学扩招的效果应在2003年及往后年份发挥出来。对不同行业的差异化作用通过\(IndustryHC_j\)反映:预期行业人力资本密集度越高,大学扩招在2003年及往后年份对行业内企业生产率的提高作用越大,即\(\beta>0\)。\(X_{ijt}\)和\(\epsilon_{ijt}\)分别表示控制变量和干扰项。
比较式(11.4)与式(11.3),根本性的区别仅在于将TCZ这一0或1变量替换为IndustryHC这一可在0-1之间连续取值的强度变量。另外一个小的差异是,式(11.4)有三个下标。我们自可以只使用行业-年份的面板数据,计算行业的生产率,这样就只有两个下标,与此前的情形类似。企业层面的数据提供了更多的变异,如果有企业的数据,利用企业数据是一个更好的选择。这并不会导致估计上太多的麻烦。如在此例中,只需注意数据中行业内企业共用同一个人力资本密集度,将个体设置为企业(而非行业),估计命令与此前给出的命令类似。
估计结果表明:Industries using more human-capital intensive technologies experienced a larger gain in TFP after 2003(见表3)。作用机制:These industries accelerated new technology adoption。异质性分析的结果:Productivity gains weaker for domestic private firms than for foreign-owned firms(见表9)。请自行阅读文中这些内容。
需要指出的是,该文汇入一个重要的讨论中。长期来看,生产率提高和经济增长大致可以划等号(短期经济增长可以来自资源再配置,如生产要素从低效率的农村流向高效率的城市)。经济增长的源泉是什么?有两种不同的理论观点:其一,良好的制度安排导致经济增长;其二,人力资本积累导致经济增长。Che and Zhang(2018)提供了支持后一种理论观点的经验证据。这不意味着前一种理论观点就不对,下一章将深入讨论前一种理论观点,并进行经验验证。
从这个例子中可以看出,双重差分法不必是分析具体政策或事件影响的雕虫小技,通过对精心挑选的政策或事件的分析,可能和重要的经济学理论关注联系在一起,回答学术界关注的问题。
该文的发现意味着,在中国人口红利已然消失的当前,增加政府教育支出,提高高等教育质量,以此增加人力资本,对促进未来中国经济增长至关重要。
参考文献
- 安格里斯特, 皮施克. 基本无害的计量经济学:实证研究者指南[M]. 格致出版社, 2012, 第5.2节.
- 范子英,李欣.部长的政治关联效应与财政转移支付分配[J].经济研究,2014,49(06):129-141.
- Cai, X., Lu, Y., Wu, M., & Yu, L. (2016). Does environmental regulation drive away inbound foreign direct investment? Evidence from a quasi-natural experiment in China. Journal of Development Economics, 123, 73-85.
- Che Y, Zhang L. Human capital, technology adoption and firm performance: Impacts of China’s higher education expansion in the late 1990s[J]. The Economic Journal, 2018, 128(614): 2282-2320.
- Li P, Lu Y, Wang J. Does flattening government improve economic performance? Evidence from China[J]. Journal of Development Economics, 2016, 123: 18-37.
- Tanaka S. Environmental regulations on air pollution in China and their impact on infant mortality[J]. Journal of health economics, 2015, 42: 90-103.