第 9 章 模型误设

本章在伍德里奇（2015）《计量经济学导论：现代观点》第五版第74-78页的基础上做了改写和拓展。

9.1 遗漏相关变量

仍然关注教育回报率。

假设真实的情况是受教育程度由高中提高到本科将使月收入提高1000元，如估计值为1500元则为高估，称产生正的偏误；估计值为800元则为低估，称产生负的偏误。

Q：如果E[IQ|受教育程度=本科]>E[IQ|受教育程度=高中]，那么，E[收入|受教育程度=本科]-[收入|受教育程度=高中]将高估、还是低估受教育程度对收入的因果影响？

本科生收入更高反映了两种影响：一个是教育的作用，另一个是本科生的IQ平均更高，而IQ高导致收入高，即收入差距一部分是由IQ差距导致的。简单求收入差值将高估受教育程度对收入的因果影响。

用数学语言讲，造成正的偏误的来源有两点：受教育程度与IQ正相关，而IQ对收入有正向的因果影响。

用计量语言概括此例：真实的模型是这样的：\(wage=\beta_0+\beta_1educ+\beta_2IQ+u,E[u|educ,IQ]=0\)。但我们错误估计了如下模型：\(wage=\alpha_0+\alpha_1educ+w\)。这属于模型误设的一种情形：遗漏相关变量。OLS估计量存在正的偏误（高估）。

一般地，真实的模型为：\(y=\beta_0+\beta_1x_1+\beta_2x_2+u\)。假设零条件均值假设成立。错误地估计模型：\(y=\alpha_0+\alpha_1x_1+w\)。\(\hat{\alpha_1}\)和\(\hat{\beta_1}\)有何联系？

推导如下：

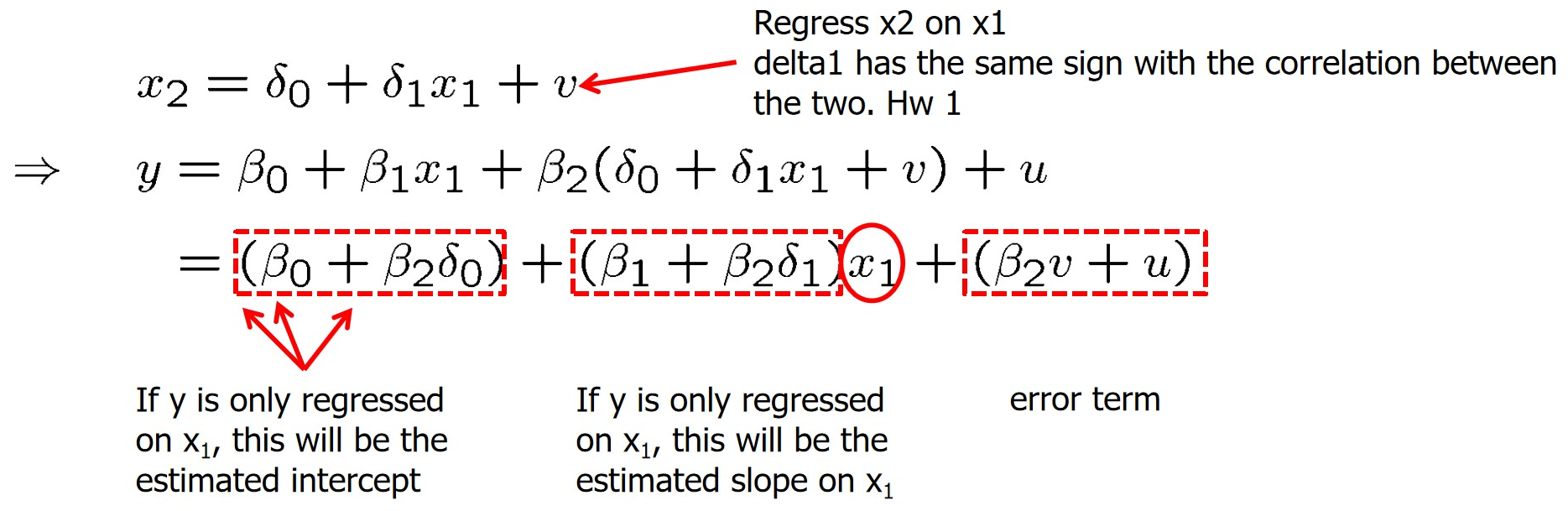
图 9.1: Derivation for omitted variables

对于真实的模型，零条件均值假设成立，故有：\(\hat{\beta_1}\stackrel{p}{\longrightarrow}\beta_1\)。而\(Cov(u,x_1)=0,Cov(v,x_1)=0\) => \(Cov(\beta_2v+u,x_1)=0\)。因此，\(\hat{\alpha_1}\stackrel{p}{\longrightarrow}\beta_1+\beta_2\delta_1\)。多出来的部分\(\beta_2\delta_1\)就是偏误。其中，\(\delta_1\)反映\(x_1\)和\(x_2\)的相关性。\(\beta_2\)反映\(x_2\)对y的因果影响。对应上面提到的两点。在例子中，\(\beta_2\)和\(\delta_1\)都为正，正正得正，偏误为正（高估）。

例: cons<-transfer+income, 遗漏income. Q: 偏误方向?

例: GDP<-govt expenditure+money supply, 遗漏货币供给. Q: 偏误方向?。

9.2 包含无关变量

假设真实的模型是：\(y=\beta_0+\beta_1x_1+\beta_2x_2+u\)。我们引入了无关变量\(x_3\)。

真实的模型又可写作：\(y=\beta_0+\beta_1x_1+\beta_2x_2+0\times x_3+u\)。通过这一改写，形式上将\(x_3\)纳入了真实模型，不再是无关变量。可推出：若零条件均值假设成立，\(x_1,x_2,x_3\)的系数的OLS估计量皆是无偏的，特别地，\(x_3\)的系数的OLS估计量的期望为0。

但要注意，包含无关变量可能使得标准误增大。

本章小结

遗漏相关变量导致偏误，包含无关变量影响方差。这两个都有问题，遗漏相关变量问题可能更大一点。所以，一般的建议是在不确定要不要加某个变量作为自变量的时候，把它加上，这可能使得标准误变大，但OLS估计量始终是无偏的，平均而言反映了因果关系。

参考文献

• 伍德里奇. 计量经济学导论(第五版)[M]. 中国人民大学出版社, 2015.