第 5 章 定性信息

5.1 二值变量

回忆OLS估计量的计算公式，不要求变量是连续的，可以是离散的，如只取两个值——1或0。称之为二值变量，或指示变量，或虚拟变量。考虑如下的二元线性回归模型：

\[\begin{align} y=\beta_0+\beta_1D+u \tag{5.1} \end{align}\]

\(\beta_1\)表示其他因素不变，D从0增加到1，y的变化。

利用OLS估计量的计算公式推出，\(\hat{\beta_1}=\bar{y}|_{D=1}-\bar{y}|_{D=0}\)。

如果零条件均值假设成立，\(\hat{\beta_1}\)是无偏的。

一个例子

中国改革的一个典型做法是先在一些地方试点，如果试点效果好，再把成功的经验推向全国。假设在中国部分地级市开展某项财税改革试点。考虑如下的计量模型：

\[\begin{align} y=\beta_0+\beta_1Pilot+u \tag{5.2} \end{align}\]

其中，y表示的是人均GDP的对数，度量经济发展水平。Pilot是一个虚拟变量，定义如下：

\[ Pilot= \begin{cases} 1& \text{进行了试点} \\ 0& \text{未进行试点} \end{cases} \]

通常把它称为政策虚拟变量（有政策为1，没政策为0，所以叫政策虚拟变量）。\(\beta_1\)表示D从0（无试点）增加到1（无试点）导致的y的变化，即试点的效果。\(\beta_1\)的OLS估计值等于试点市y的平均值减去未试点市y的平均值。如果零条件均值假设成立，OLS估计量是无偏的。零条件均值假设成立的一种情形是试点城市的选定是随机的。

5.2 虚拟变量陷阱

定义虚拟变量NoPilot如下：

\[ NoPilot= \begin{cases} 1& \text{未进行试点} \\ 0& \text{进行了试点} \end{cases} \]

Q：可以在计量模型中同时加入Pilot和NoPilot吗？即可以设置如下的计量模型吗？

\[\begin{align} y=\beta_0+\beta_1Pilot+\beta_2NoPilot+u \tag{5.3} \end{align}\]

\(Pilot+NoPilot=1\)。存在多重共线性。因此，不能这样做。

5.3 分类、基准和虚拟变量

从分类的角度理解虚拟变量。将地级市分成两类：试点和未试点。以未试点的地级市为基准，给试点的地级市一个虚拟变量Pilot（如图5.1）。回归中Pilot的系数表示相对基准，试点地级市因变量的平均增幅.

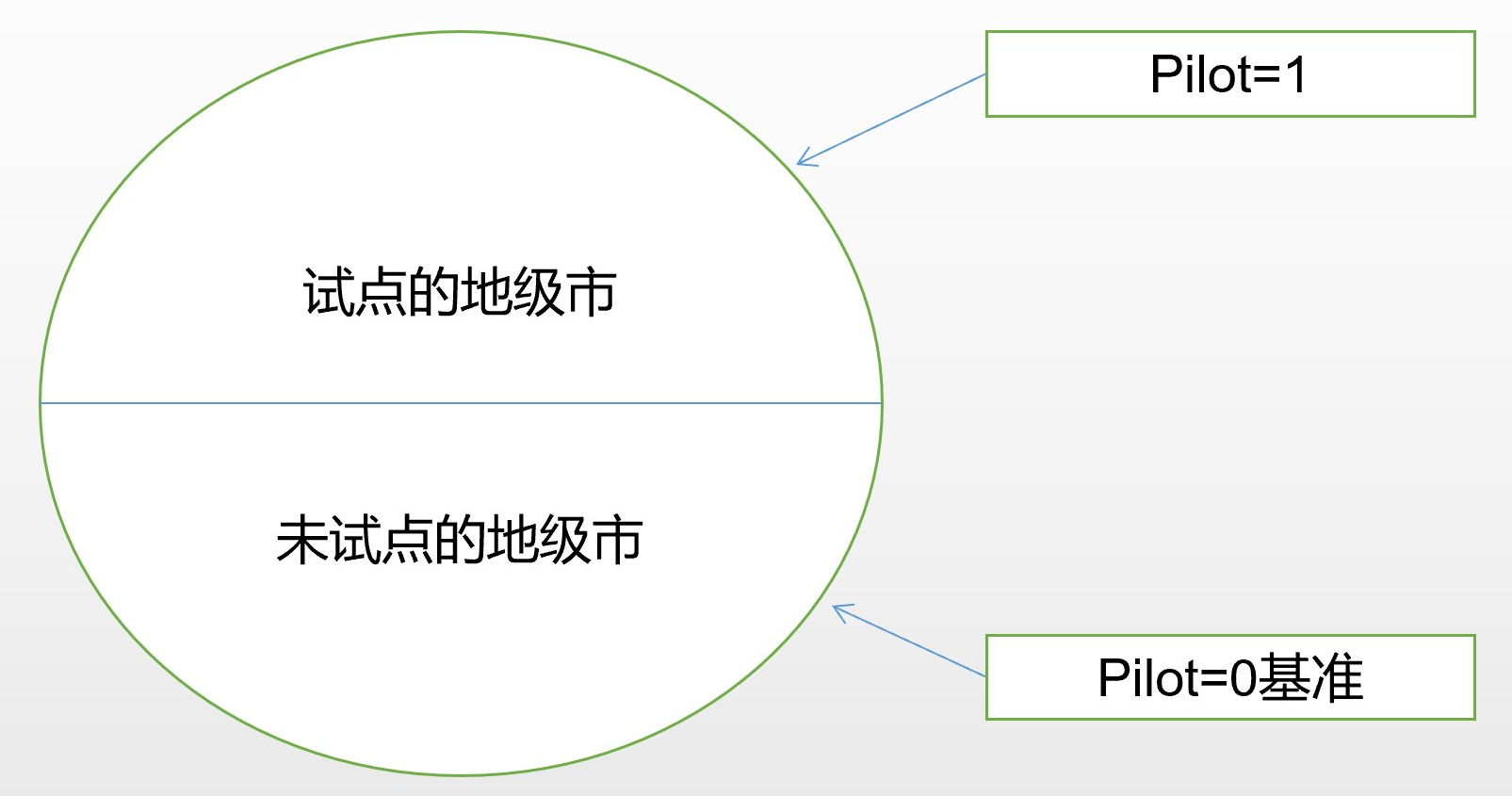
Classification

图 5.1: Classification

基准的选择是任意的。也可以选择试点的地级市作为基准，给未试点的地级市一个虚拟变量NoPilot，估计\(y=\beta_0+\beta_1NoPilot+u\)。从数学上讲，这样做没有问题，但NoPilot的系数的含义不那么自然。

5.4 多个虚拟变量

考虑另外一种试点情形：有两套试点方案，一套试点方案在一些地区实施，另一套试点方案在另一些地区实施，还有一些地区未实施任一方案。由于有两套试点方案，需要定义两个虚拟变量。记第一种试点方案的虚拟变量为Pilot1（试点此方案记为1，否则记为0），第二种试点方案的虚拟变量为Pilot2。计量模型：

\[\begin{align} y=\beta_0+\beta_1Pilot1+\beta_2Pilot2+u \tag{5.4} \end{align}\]

\(\beta_1\)和\(\beta_2\)分别表示试点方案1和2的效果。

\(\beta_1\)的OLS估计量：推行第一种试点方案的地级市y的均值-未试点的地级市y的均值。\(\beta_2\)的OLS估计量：推行第二种试点方案的地级市y的均值-未试点的地级市y的均值。

也可以从分类的角度理解，如图5.2。

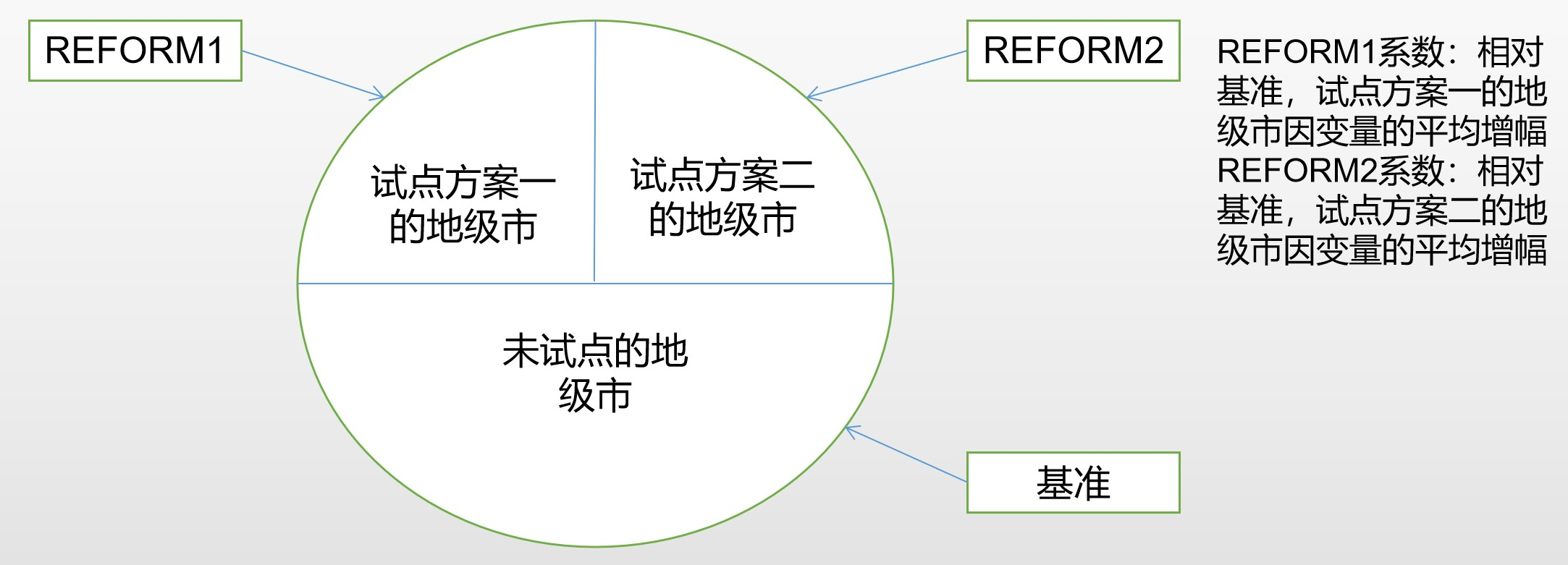
Classification (continued)

图 5.2: Classification (continued)

把地级市分成三类：没有进行试点的地级市，试点方案一的地级市，试点方案二的地级市。把未进行试点的地级市作为基准。给试点方案一的地级市一个虚拟变量Pilot1，其系数表示相对基准试点方案二的地级市因变量的平均增或减幅。 给试点方案二的地级市一个虚拟变量Pilot2，其系数表示相对基准试点方案二的地级市因变量的平均增或减幅。

5.5 更多例子

用虚拟变量可以做很多事。比如，定义一个虚拟变量Male。顾名思义，它是男性的虚拟变量，赋值如下：

\[ Male= \begin{cases} 1& \text{男} \\ 0& \text{女} \end{cases} \]

计量模型：

\[\begin{align} wage=\beta_0+\beta_1Male+u \tag{5.5} \end{align}\]

Q：\(\hat{\beta_1}=?\)

还可以用虚拟变量研究种族（汉族还是少数民族）；行业（重工业或轻工业，或三大产业）；地区（东中西）。

伍德里奇《计量经济学导论：现代观点》第五版第7.1-7.3节对定性信息做了更详尽的介绍。

参考文献

  • 伍德里奇. 计量经济学导论(第五版)[M]. 中国人民大学出版社, 2015.