第 10 章 面板数据模型：计量方法及应用

再次考虑教育回报率的例子。如果我们有IQ的数据，直接把它放到回归模型中，作为一个额外的自变量就可以了。相当于比较具有相同IQ、不同受教育程度的人（回忆多元回归模型中系数的含义）。

问题是，我们可能没钱度量IQ。在没钱度量IQ的情况下，有什么别的思路控制IQ的影响以准确地估计教育回报率吗？

世纪佳缘创始人龚海燕高二辍学到电子厂打工，收入微薄，后重拾学业，自复旦毕业后收入大幅提高。收入增加不是IQ引起的，因为同一个人（青少年之后）IQ不变，更可能是再教育之于她的回报。这里的关键在于，我们关注同一个人收入的变化，从而排除了其不变的IQ的影响。

总之，如果知道IQ，可比较具有相同IQ的不同个体的收入；如果不知道IQ，可比较同一个IQ不变的人再教育前后的收入。后者是我们接下来要学习的面板数据估计的关键。

斯托克和沃森（2012，第10章）结合例子对面板数据做了精彩的介绍。参考其文，本章做了精炼和拓展。

10.1 面板数据的定义

简单来说，n个个体在T个时期的数据构成面板数据。有两个维度：一个时间维度，一个空间维度。可以写成下面的形式：

\[ (X_{it},Y_{it})\ \ i=1,2,…,n\ \ t=1,2,…,T \]

X和Y是变量。两个下标中，i表示个体，t表示时间。因此，样本总量为\(n\times T\)。

例：江苏省13个地级市2016-2018年的经济数据构成1个面板数据。这里共有13个个体，n=13；三年，T=3。观测值数量就是\(13\times 3=39\)。

10.2 差分法

斯托克和沃森（2012，第10章）基于美国州面板数据，研究啤酒税对交通死亡率的影响。预期为负向影响，因为啤酒税提高，啤酒消费量降低，酒驾减少，交通事故减少，交通死亡率降低。

啤酒税的单位为dollars per case，记为X。交通死亡率定义为每万人中因交通事事故死亡的人数，记为Y。

如果像以前一样，使用一年的横截面数据，如1982年的数据，结果显示：啤酒税的估计系数为0.15，符号与预期不符；换用1988年的数据进行回归，啤酒税的估计系数为0.44，依然是正的，不太合理。

为什么会这样？一个可能的解释是，模型遗漏了重要的因素，导致高估。一个可能的遗漏因素是酒驾的社会接受度。各州对酒驾的接受程度不一样。酒驾的社会接受度（正向）影响交通死亡率。同时，有可能酒驾的社会接受度高的地方，政府缺钱，对啤酒征重税。因此，偏误为正（高估）。

如果能度量酒驾的社会接受度, 将之加入计量模型：

\[\begin{align} Y_{i1982}=\beta_0+\beta_1X_{i1982}+\beta_2Z_i+u_{i1982} \tag{10.1} \end{align}\]

\[\begin{align} Y_{i1988}=\beta_0+\beta_1X_{i1988}+\beta_2Z_i+u_{i1988} \tag{10.2} \end{align}\]

\(Z_i\)表示酒驾的社会接受度，只有个体（州）下标，反映为在任一给定的州内它不随时间变化。它是啤酒税之外的另一个解释变量。社会态度变化缓慢，可能几十上百年才会有明显的转变。而研究者收集到的数据的时间段往往较短。在较短的时间段内，可以认为社会态度保持不变。注意，在样本时间段内，尽管同一个州的\(Z_i\)保持不变，不同州的\(Z_i\)一般不一样。

用交通死亡率对啤酒税和酒驾的社会接受度回归，可以解决原来由\(Z_i\)造成的遗漏变量问题。可惜问题在于，很难度量酒驾的社会接受度。Q：在观测不到\(Z_i\)但知它不随时间变化的情况下，如何估计\(\beta_1\)？我们不知道\(Z_i\)，又希望控制\(Z_i\)的影响。注：我们不关心\(\beta_2\)。[提示：回顾本章开头的例子]

在本章开头的例子中，我们关注同一个人收入的变化，排除了其不变的IQ的影响，用再教育之后的收入减去之前的收入作为教育回报率的估计。这里，无非是个体变了，不再是个人，而是州。我们想控制的变量从不变的IQ变成了不变的\(Z_i\)。类似地，我们关注同一个州交通死亡率的变化，排除了其不变的\(Z_i\)的影响，用后边1988年的交通死亡率减去前边1982年的交通死亡率：

\[\begin{align} (Y_{i1988}-Y_{i1982})=\beta_1(X_{i1988}-X_{i1982})+(u_{i1988}-u_{i1982}) \tag{10.3} \end{align}\]

变成不含常数项的的简单回归模型。因变量是1982-1988年交通死亡率的变化。自变量是1982-1988年啤酒税的变化。应用2.5OLS估计量的计算公式，\(\beta_1\)的估计系数为-1.04，变成负的，符号符合预期。

What if T>2？计量模型写作：

\[\begin{align} Y_{it}=\beta_0+\beta_1X_{it}+\beta_2Z_i+u_{it} \tag{10.4} \end{align}\]

或

\[\begin{align} Y_{it}=\beta_1X_{it}+\alpha_i+u_{it},\ \alpha_i\equiv\beta_0+\beta_2Z_i \tag{10.5} \end{align}\]

实际上，除了酒驾的社会接受度以外，地理（记为G）也会影响交通死亡率。山路十八弯更容易发生交通事故。地理也可能跟啤酒税相关。并且，地理不随时间变化。考虑地理等影响交通死亡率、可能和啤酒税相关又不随时间变化的因素，模型拓展为：

\[\begin{align} Y_{it}=\beta_1X_{it}+\alpha_i+u_{it},\ \alpha_i\equiv\beta_0+\beta_2Z_i+\beta_3G_i+... \tag{10.6} \end{align}\]

称\(\alpha_i\)为个体固定效应，表示所有观测不到、不随时间变化的因素对因变量的综合影响。它只有一个下标i，没有时间下标，反映它不随时间变化（同一个体各期取值相同）、随个体变化（不同个体的值不一样）。

原则上来讲，我们可以关注同一个州各期相比前一期的变化：

\[\begin{align} (Y_{it}-Y_{it-1})=\beta_1(X_{it}-X_{it-1})+(u_{it}-u_{it-1}) \tag{10.7} \end{align}\]

10.3 去均值法

除了关注同一个州各期相比前一期的变化，我们还可以关注同一个州各期相比该州平均值的变化。后一种处理应用更广。它将估计分成两步：第一步，每个变量减去个体均值；第二步，利用“个体中心化”的变量进行估计。具体操作如下：

去均值法

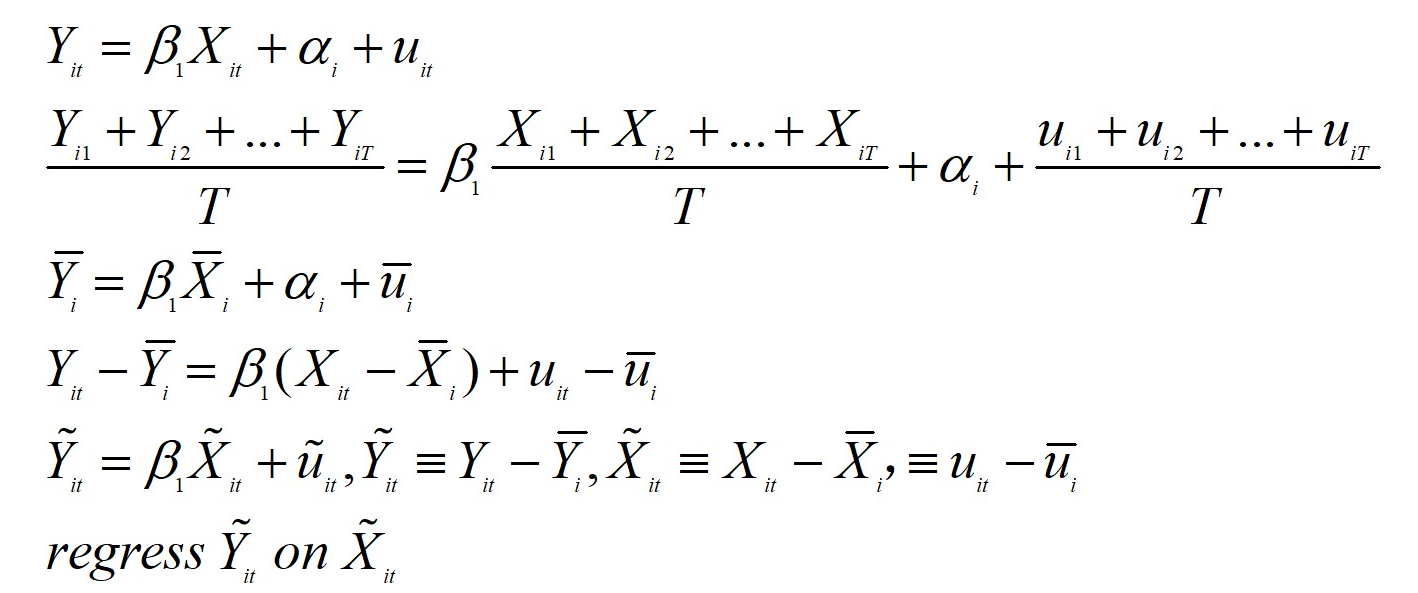
图 10.1: 去均值法

最后，模型退化为一个不含常数项的简单回归，此情形下OLS估计量的计算公式见2.5，可据此估计参数。

Stata提供了一个命令来完成这一系列工作，是为：

xtreg Y X, fe

应用于美国各州1982-1988年的数据，啤酒税的估计系数为-0.66，符号符合预期（斯托克和沃森，2012，第10章）。

10.4 固定效应模型

对于式(10.6)，无论是应用差分法还是去均值法均允许\(\alpha_i\)与\(X_{it}\)相关——\(\alpha_i\)最终被消掉了，它与\(X_{it}\)相关性不构成问题。

称允许\(\alpha_i\)与\(X_{it}\)相关的式(10.6)为固定效应模型。需要强调的是，不是有个体固定效应就是固定效应模型，有个体固定效应且它可以和自变量相关才是。

10.5 LSDV法

式(10.6)中\(\alpha_i\)可以写成：

\[\begin{align} \alpha_i=\alpha_1D_1+\alpha_2D_2+...+\alpha_nD_n \tag{10.8} \end{align}\]

其中，\(D_1\)是第一个州的虚拟变量：

\[ D_1= \begin{cases} 1& \text{第一个州（所有时期）} \\ 0& \text{其他州（所有时期）} \end{cases} \]

\(D_2\)是第二个州的虚拟变量。以此类推。请自行验证式(10.8)成立。

于是，式(10.6)可以写成:

\[\begin{align} Y_{it}=\beta_1X_{it}+\alpha_1D_1+\alpha_2D_2+...+\alpha_nD_n+u_{it} \tag{10.9} \end{align}\]

这是一个多元回归。自变量包括X和n个虚拟变量。可用如下的多元回归命令估计：

regress Y X D2 … Dn

这一估计得到的\(\hat{\beta_1}\)与由去均值法算得的\(\hat{\beta_1}\)相同。

称该法为LSDV法。LS指最小二乘，DV指虚拟变量。该法有一个缺点：当n很大时，自变量的个数（在本例中为1+n）很大，会增大运算量。差分法和去均值法不存在这一问题。

10.6 时间固定效应

斯托克和沃森（2012，第10章）认为，除了上面提到的影响交通死亡率的因素外，汽车行业全国安全标准也会影响交通死亡率。随着时间推移，汽车行业全国安全标准提高（如从不要求配备安全气囊到要求配备安全气囊），有利于降低交通事故的死亡率。

汽车行业全国安全标准提高发生在全国范围内，能减少所有州的交通死亡率。假设汽车行业全国标准提高使所有州交通死亡率降低相同幅度是合理的。

记汽车行业全国安全标准为\(S_t\)。它只有一个时间下标t，没有个体下标，反映安全标准随时间变化，但在任一个时间点对所有州都是一样的。将其纳入计量模型：

\[\begin{align} Y_{it}=\beta_1X_{it}+\beta_3S_t+\alpha_i+u_{it} \tag{10.10} \end{align}\]

汽车行业全国安全标准对所有州的影响都为\(\beta_3S_t\)。预期\(\beta_3\)的系数为负。注意如果\(S_t\)和\(X_{it}\)相关，不将\(S_t\)加入计量模型将导致OLS估计量出现偏误。

如果\(S_t\)可观测，无非就是增加一个解释变量。但，很可能\(S_t\)不可观测。Q：怎么处理？

将计量模型写成：

\[\begin{align} Y_{it}=\beta_1X_{it}+\alpha_i+\lambda_t+u_{it},\ \lambda_t\equiv\beta_3S_t \tag{10.11} \end{align}\]

除了汽车行业全国安全标准，全国石油价格也影响交通死亡率，因为油价贵了，大家开车少，事故少。等等。一般地，\(\lambda_t\)包含所有随时间变化但不随个体变化的影响因素，称为时间固定效应。

Q：Y为经济增长率，个体固定效应包含哪些因素？时间固定效应又包含哪些因素？

类似10.5，\(\lambda_t\)可以写成：

\[\begin{align} \lambda_t=\lambda_1E_1+\lambda_2E_2+...+\lambda_TE_T \tag{10.12} \end{align}\]

\(E_1\)是第1期的虚拟变量。\(E_2\)是第2期的虚拟变量。以此类推。

于是，式(10.11)可以写成:

\[\begin{align} Y_{it}=\beta_1X_{it}+\alpha_i+\lambda_1E_1+\lambda_2E_2+...+\lambda_TE_T+u_{it} \tag{10.13} \end{align}\]

为估计该式，可使用如下的Stata命令：

xtreg Y X E2 … ET, fe

如果在Stata数据中，有一个名为year的变量，记录年份，那么，更简便的Stata命令是

xtreg Y X i.year, fe

“i.year”将为变量year中的每一年生成一个虚拟变量，即生成E2、…、ET。

估计结果显示，\(\beta_1\)的估计系数是-0.64，符合预期。

控制变量

尚有其他因素影响交通死亡率。例如，斯托克和沃森（2012，第10章）指出，一个可能的影响因素是平均而言司机开车熟练程度，可用司机平均驾驶里程度量。把诸如此类的变量加进来能够尽可能地缓解遗漏变量问题。

注意：加入的控制变量须随时间变化，因为凡不随时间变化的因素都在差分或去均值时被减掉了。也就是说，固定效应模型无法估计不随时间变化的变量的作用。

10.7 应用：财政联邦主义的文献

第一代财政联邦主义

财政联邦主义研究财权和事权在各级政府之间如何分配。第一代财政联邦主义认为，全国性公共品，应作为中央政府的事权；而地方性公共品，应作为地方政府的事权，因为地方政府掌握更多信息，包括当地居民的偏好和公共品供给的成本。进一步引申提出，适度分权能提高效率，进而促进经济增长。

大量文献从经验层面检验财政分权与经济增长的关系。

Davoodi and Zou (1998) use a panel data set of 46 countries over the 1970-1989 period to investigate the relationship between fiscal decentralization and economic growth.

他们使用如下的固定效应模型：

\[ g_{it}=\delta_1+\delta_2\theta_{it}+\delta_3\tau_{it}+\delta_4^{'}D_i+\delta_5{'}N_t+\delta_6{'}X_{it}+\epsilon_{it} \]

  • i and t refer to country i at time t。i=1,2…,46。t=1对应1970-79年，=2对应1980-89年。注意一期是十年；
  • g is the average growth of real per capita output over ten-year periods。注意作者关注长期（十年）经济增长。实际值=名义值/价格指数；
  • \(\theta\) is the measure of fiscal decentralization, defined as the subnational share of total government spending。这是核心解释变量。以一个例子说明其取值：如果一国各级政府支出为100，其中40由地方政府支出，则该变量等于0.4；
  • \(\tau\) is the tax rate, defined as the ratio of total tax revenues to GDP；
  • \(D_i\)是个体（国）虚拟变量构成的一个向量，\(\delta_4^{'}D_i\)就等于个体固定效应；
  • 与上一点类似，\(\delta_5{'}N_t\)等于时间固定效应；
  • X是控制变量, 包括: the average growth rate of population；initial human capital；initial per capita GDP; and the average real investment share of GDP。这些常被认为是经济增长的决定因素。

作者区分发达国家和发展中国家进行了估计，即使用发达国家的数据做一次估计，同时使用发展中国家的数据做一次估计。这是异质性分析（见7.2）。

发达国家的估计结果见图10.2，发展中国家的估计结果见图10.3。两表中，首列是变量名，列（1）-（5）每一列是一个回归，区别在于控制变量逐渐增多。对估计结果总结如下：We find a negative relationship between fiscal decentralization and growth in developing countries, but none in developed countries。

Results for developed countries

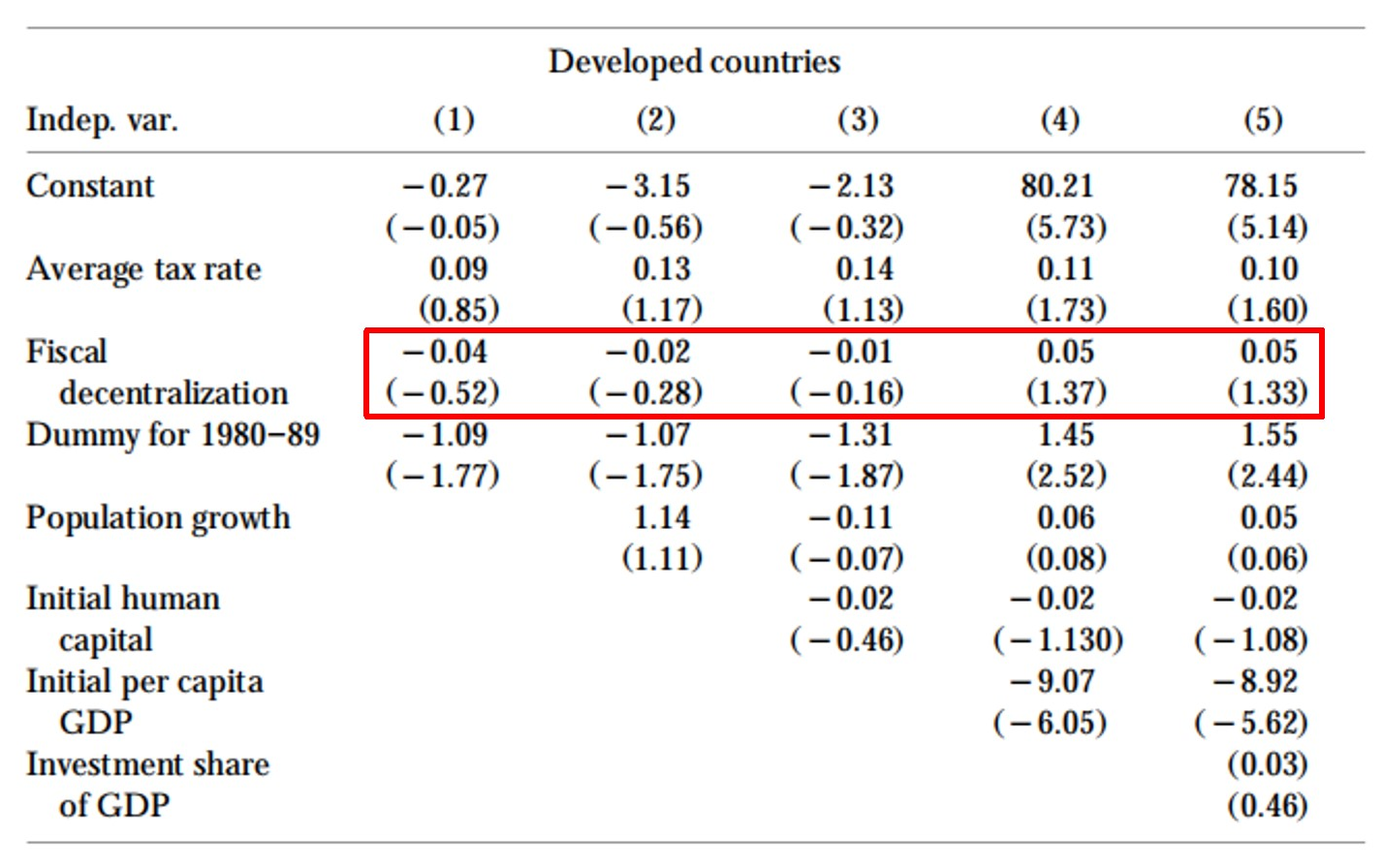
图 10.2: Results for developed countries

资料来源：Davoodi and Zou（1998）表2。

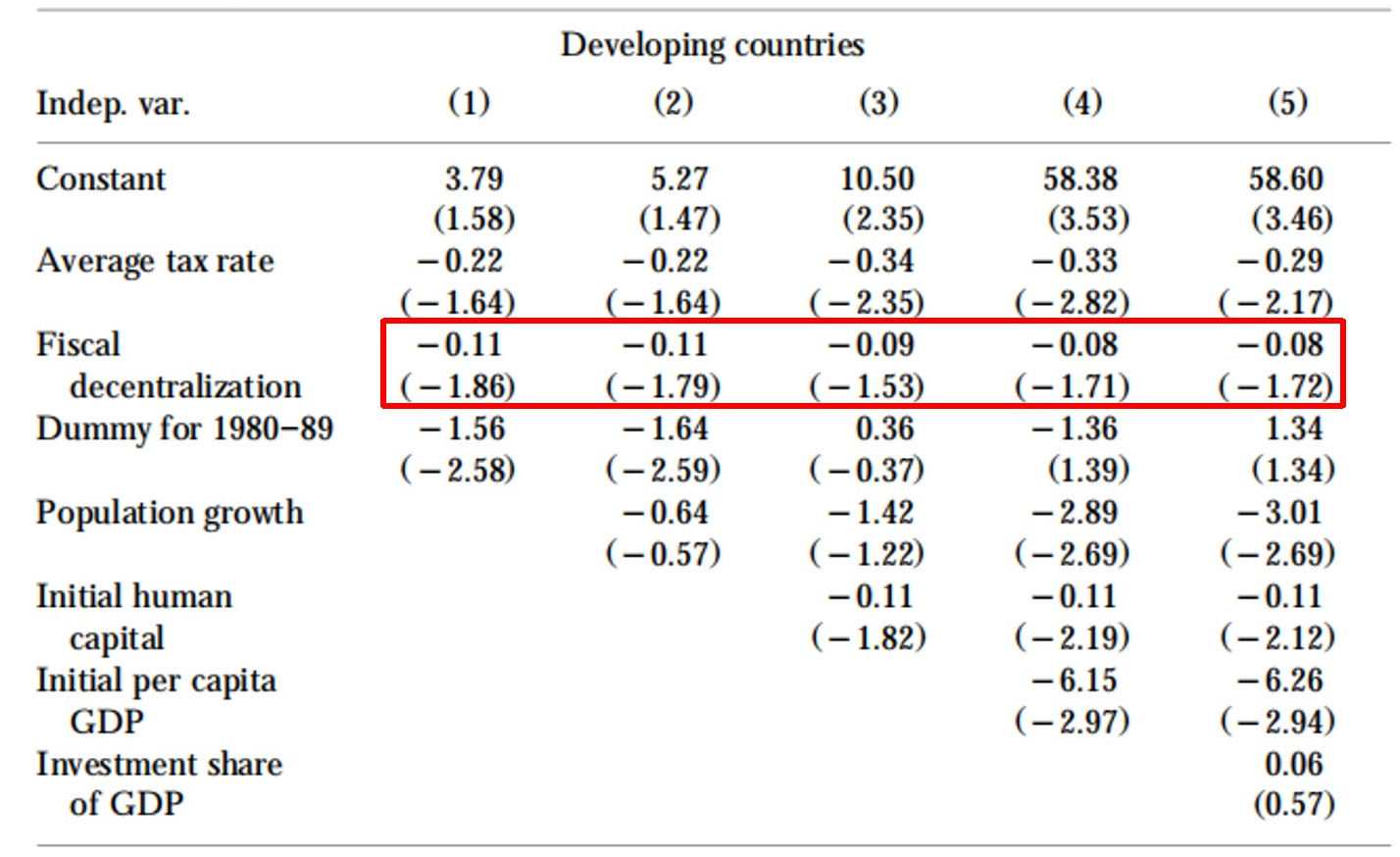
Results for developing countries

图 10.3: Results for developing countries

资料来源：Davoodi and Zou（1998）表2。

除这篇文章以外，还有大量研究财政分权和经济增长关系的经验文献。这些文献的结果各异，有的发现财政分权促进了经济增长，有的则得出相反的结论。这些相悖的经验结果不支持上述理论。这引人反思：上述理论正确吗？

第一代财政联邦主义隐含地假设：地方政府是良善的（最大化辖区居民的福利）。惟其如此，将地方公共品交由地方政府提供，才能期望它们利用信息优势，提高效率。现实中，地方政府可能扮演两种不同的角色：扶持之手（helping hand），如改革开放后中国地方政府不断改善营商环境；攫取之手（predatory hand），如索马里地方政府所做的那样。

地方政府的行为取决于地方政府面临的激励。在此认识的基础上发展出第二代财政联邦主义，它强调财政激励。

第二代财政联邦主义

第二代财政联邦主义强调财政激励，尤其是边际收入分成率（marginal revenue retention rate），它指政府收入在边际上增加1单位，地方能存留多大比例。如某省从某企业收上来1单位税收，其中0.3单位上缴中央国库，剩下的0.7存留几用，则该省的边际收入分成率为0.7。预期边际收入分成率越高，地方政府越有激励发展地方经济，扮演扶持之手的角色。

Jin et al.（2005）检验了中国财政包干制时期财政激励对经济发展的影响。该时期央地之间的财政包干制有多种安排，故不同省份有不尽相同的边际收入分成率。基于此，构建如下的固定效应模型：

\[ Y_{it}=\alpha_i+\gamma_t+\delta^{'}Z_{it}+\sigma^{'}W_{it-1}+u_{it} \]

  • i表示省份；
  • t表示年份，从1982到1992年；
  • \(Y_{it}\) is a vector of variables measuring the development of the non-state sector and reform in the state sector in a province
  • \(Z_{it}\) 包括边际收入分成率和财政分权指标；
  • \(\alpha_i\)是省份固定效应；
  • \(\gamma_t\) are the year dummies, which are intended to capture the effects of nationwide macroeconomic fluctuation；
  • \(W_{it-1}\) is the lagged per capita GDP；
  • \(u_{it}\)是干扰项。

作者首先考察财政激励对非国有部门的影响，结果如图10.4所示。在Panel A中，因变量为growth of rural enterprise employment；在Panel B中，因变量为growth of non-state-non-agricultural employment。以列（2）为例，自变量包括边际收入分成率、滞后一期的人均GDP、省份固定效应和年份虚拟变量。结果表明，边际收入分成率越高，非国有部门就业增长越快。

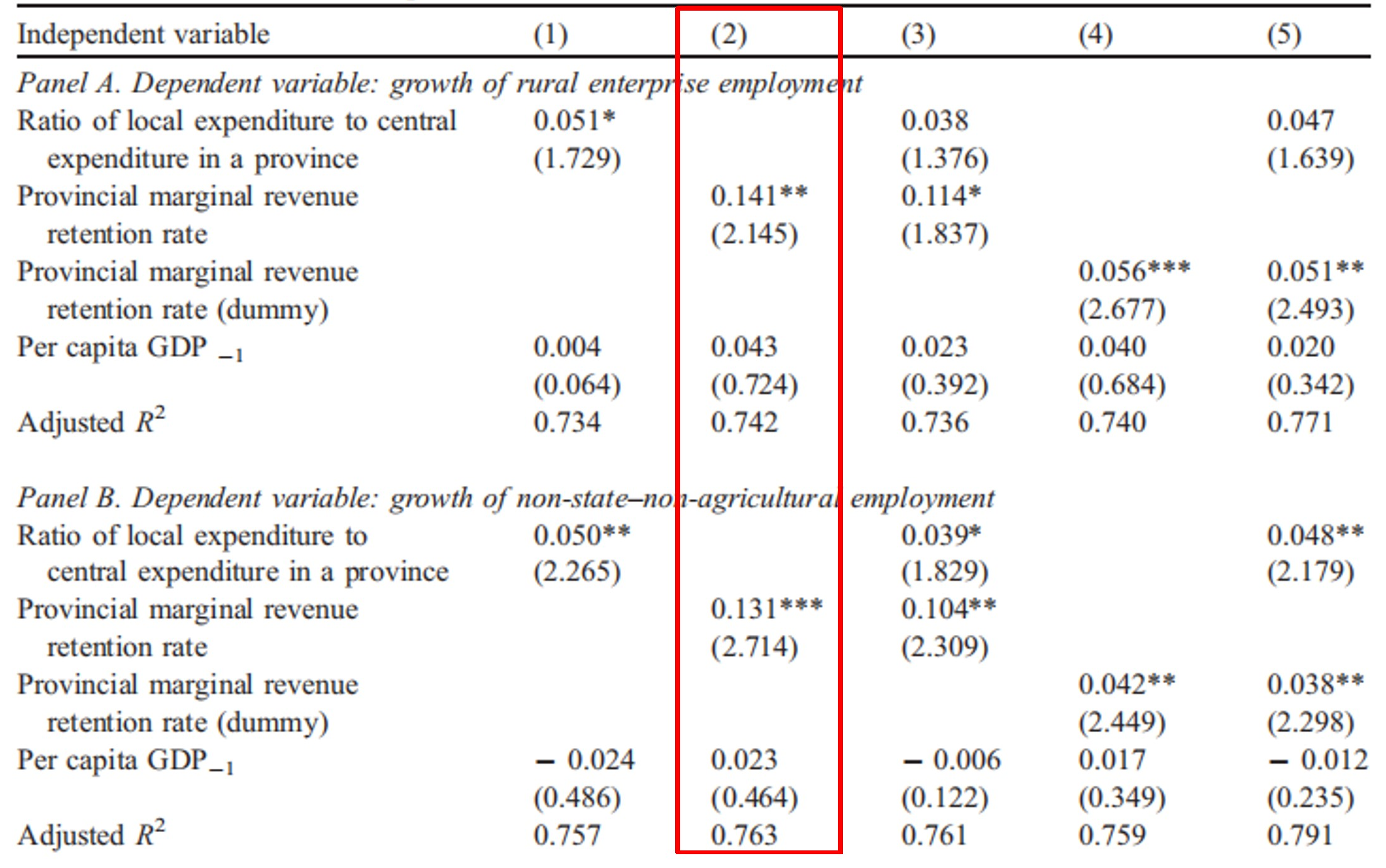
Fiscal incentives and the development of the non-state sector

图 10.4: Fiscal incentives and the development of the non-state sector

资料来源：Jin et al.（2005）表5。

非国有部门的发展是否倒逼国有企业改革？带着这个问题，作者进一步考察财政激励对国有部门改革的影响，结果如图10.5所示。在Panel A中，因变量为change in the share of contract workers in total state employment；在Panel B中，因变量为change in the share of bonuses in total employee wages。仍以列（2）为例，结果表明，边际收入分成率提高使得国有部门的合同工占比提高，奖金占比提高，即促进了国有部门的市场化改革。

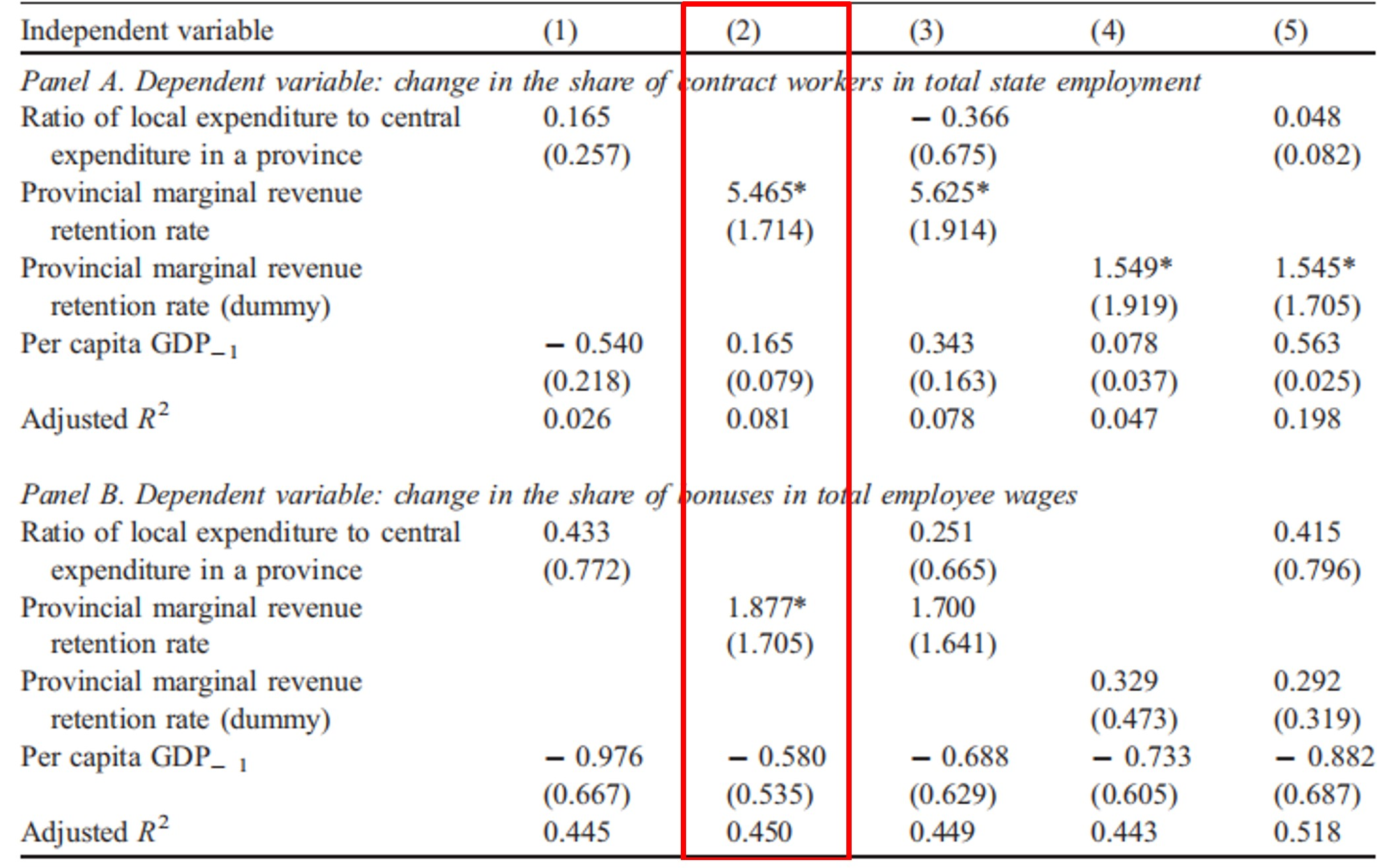
Fiscal incentives and the reform of the state sector

图 10.5: Fiscal incentives and the reform of the state sector

资料来源：Jin et al.（2005）表6。

本章小结

固定效应模型控制了不可观测、但不随时间变化的影响因素（如酒驾的社会接受度）以及不可观测、但不随个体变化的影响因素（如汽车行业的全国安全标准），进一步缓解了遗漏变量问题。但是，它不能处理不可观测、既随时间变化又随个体变化的因素。比如，在交通死亡率的例子中，雨雪天气容易引发交通事故，出现频率高，交通死亡率就高。这未被纳入计量模型。诸如此类的遗漏因素可能与（核心）解释变量相关，导致OLS估计量有偏。

总之，固定效应模型缓解了遗漏变量问题，但不能保证彻底解决遗留变量问题，OLS估计量依然可能是有偏的。但存在一种特殊的情形，在满足一定可验证的条件时，可以确定OLS估计量能够识别因果关系，这就是接下来要讲的双重差分法，它是固定效应模型的一个特例。

参考文献

  • 斯托克, 沃森. 计量经济学(第三版)[J]. 格致出版社, 2012, 第10章.
  • Davoodi H, Zou H. Fiscal decentralization and economic growth: A cross-country study[J]. Journal of Urban economics, 1998, 43(2): 244-257.
  • Jin H, Qian Y, Weingast B R. Regional decentralization and fiscal incentives: Federalism, Chinese style[J]. Journal of public economics, 2005, 89(9-10): 1719-1742.