第 1 章 导论

1.1 相关和因果关系

（1）相关关系和因果关系的定义与对比

What is Correlation?

Ansari（2022）：

Correlation is a relationship or connection between two or more objects. If X and Y, two variables, tend to be observed at the same time, there’s a correlation between them. You cannot say X caused Y, you will simply say that when X and Y are observed together.
Positive Correlation: When variable X increases, variable Y also increases. Similarly, if X decreases, Y correspondingly decreases.
Negative Correlation: When variable X increases, variable Y decreases, or vice versa.
No Correlation: Any change in X leads to no change in Y, or vice versa.

Analytica（2019）：

A correlation is a statistical measure that we use to describe the linear relationship between two continuous variables.

What is Causation?

Ansari（2022）：

Unlike Correlation, the relationship is not because of a coincidence. We are saying that X causes Y, or vice versa. It means that the existence of one variable causes the manifestation of another.

“cause”是什么意思？这里所谓导致是指其他条件不变的情况下，如果X变化，Y也随之变化，那么我们就说X导致了Y，X和Y具有因果关系（X->Y的因果关系）。在微观经济学中，需求函数就是说价格和需求之间存在负向因果关系：如果价格提高，需求会减少。隐含的假设是，价格提高的时候，其他因素（包括偏好、其他商品的价格和收入等）一概不变，这时需求才会减少。如果价格提高的时候，收入也提高，需求不一定减少。

What’s the difference between correlation and causation?

Madhavan（2019）：

Causation explicitly applies to cases where action A causes outcome B. On the other hand, correlation is simply a relationship. Action A relates to Action B—but one event doesn’t necessarily cause the other event to happen.
However, we cannot simply assume causation (注：A->B) even if we see two events happening, seemingly together, before our eyes. One, our observations are purely anecdotal. Two, there are so many other possibilities for an association, including but not limited to:

  • 反过来：B导致A。反向因果。
  • A和B相关，但它们均由C所致。例：图 1.1。在该图中，溺死数和冰淇淋消费量是相关关系，而非因果关系。实际上，是天热导致溺死数和冰淇淋消费量同时增加=>遗漏变量
  • 另一种情形：A->B, C->B，A和C相关。 A和B之间的相关关系在部分程度上由C导致。例：A是受教育程度，B是毕业后的收入。通常，我们观测到，受教育程度更高的人的平均收入也更高。但是，其高收入并不完全由教育导致，还可能有别的因素起作用：如受教育程度更高的人的平均IQ更高，高的IQ也会导致高收入=>遗漏变量。
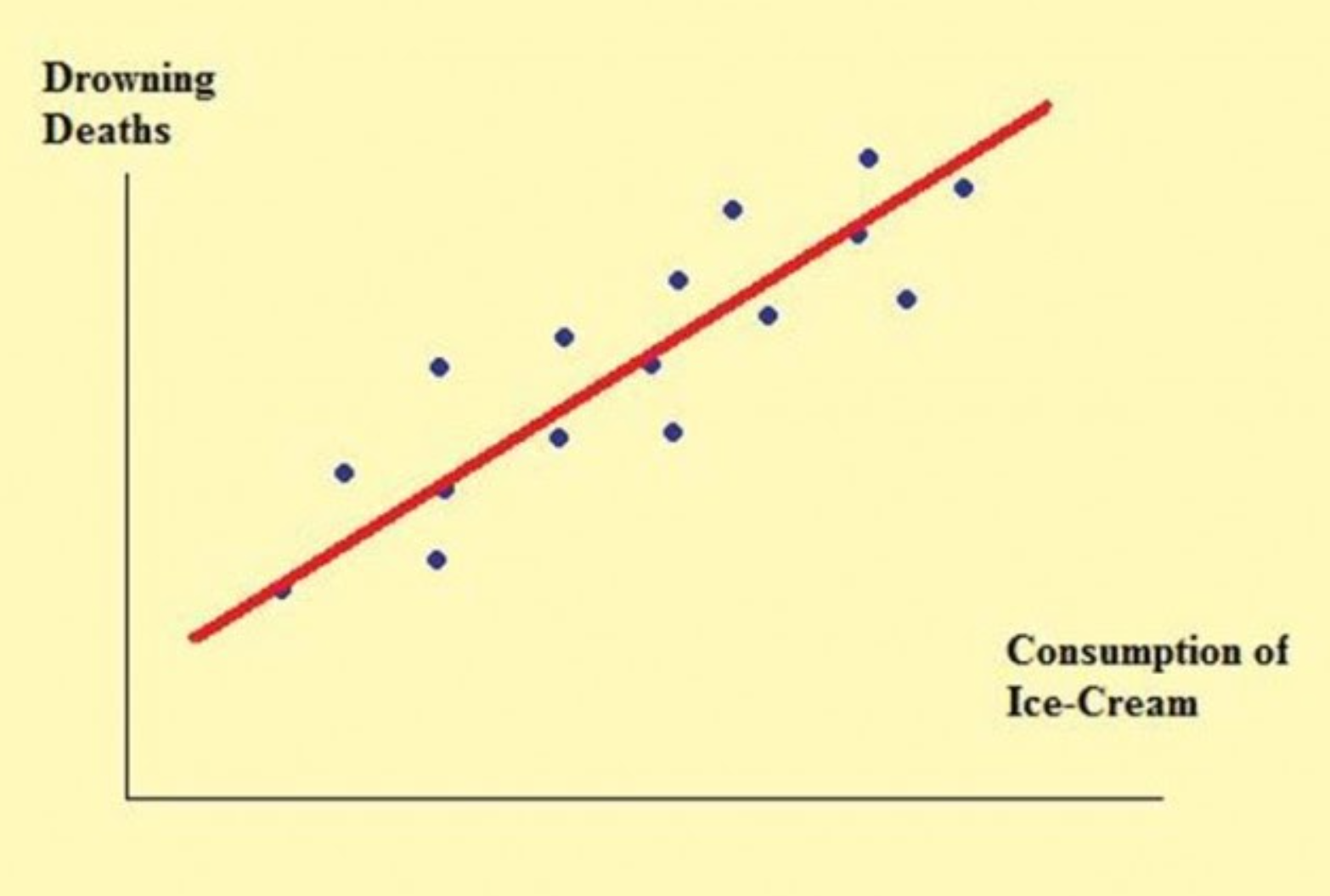
Drowning deaths and ice-cream consumption

图 1.1: Drowning deaths and ice-cream consumption

资料来源：Ansai（2022）。

判断正误

Correlation => Causation. False.

Causation => Correlation. False: think of nonlinear causation.

测试题

题目1: 在美国金融危机后，我国推出了“四万亿”投资，经济随之企稳，如图 1.2 所示：

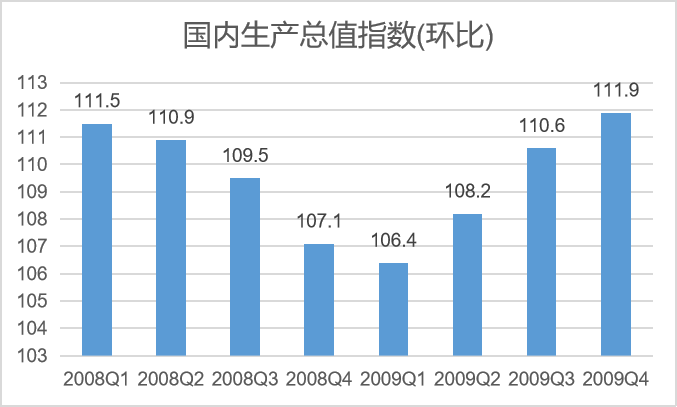
Economic growth rate: 2008-2009

图 1.2: Economic growth rate: 2008-2009

Q: “四万亿”投资与GDP增长率(2019Q1->2019Q4)提高5.5%是（前者->后者的）因果关系吗?

题目2: 相比西部地区，东部地区基础设施存量多1万亿（假设值）, 人均GDP高2万元（假设值）。Q: 前者与后者是（前者->后者的）因果关系吗?

（2）识别因果关系

何为识别因果关系？把确定两个变量之间是否具有因果关系的过程叫做识别因果关系，在英文里面叫做”identification”。

识别因果关系的经典方法:随机实验法

识别因果关系的经典方法：随机实验法，在英文里面叫做random experiment。借鉴自自然科学，核心是随机分组。比如，研究肥料对作物收成的影响。这里指因果关系含义上的影响。隐含的假设是，只肥料这一个因素改变——肥料增加1单位，其他影响作物收成的因素（包括土地质量、降雨量、寄生物等）均保持不变，大豆的产出增加多少？用随机实验处理这个问题的思路：找到若干块土地，如100块，每块土地的大小都是一样的，如1亩。将这些土地随机分成两组。因为是随机分组，所以这两组土地的情况平均来说是相同的。然后对其中一组不施肥，对另外一组施1单位的肥料。用施肥组的平均作物收成减去不施肥组的平均作物收成，看它为正还是为负，藉此判断肥料对作物收成的影响。

这一差值反映了因果关系。为何？回忆：因果关系是说其他因素不变，只肥料变化作物产出如何变化。这里，因为分组是随机的，两组的情况平均而言是相同的，仅肥料使用量有异。所以，作物收成的差异平均而言反映了施肥量的影响。

于社会科学而言随机实验法的局限

局限其一。试看下例。教育回报率指受教育程度提高，比如说受教育程度从高中提高到大学，会使得收入如何变化？这是一个因果关系含义上的概念。隐含的假设是，受教育程度提高时其他影响收入的因素（IQ、家庭环境等）都保持不变。如果用随机实验法，做法是：找一些小孩，随机地给他们不同年限的教育，继而比较他们成年后的收入。因为他们的受教育年限是随机的，所以他们成年后的收入差异（平均而言）反映了受教育年限的差异。但是，这里存在道德伦理方面的问题：为什么给一些小孩更高的教育年限，而给另外一个小孩更低的教育年限。对此很多人不会认同。一般地，从伦理道德的角度，很多时候随机实验法在社会科学中不可行。

局限其二。仍看一例。研究交通基础设施对经济增长的影响。用随机实验法处理这一问题：去落后地区找一些不通路的村子，如找100个村子。将其随机分成两组，一些给修路，一些不给修路。然后看那些给修路的村子在路通之后经济发展是否更好。问题在于，修路贵。给50个村修路，即使不花几千万也得花几百万。哪个研究者有这么多钱搞这个研究？随机实验法成本高，故需开发具备经济性的计量方法识别因果关系。

总之，本书的核心就是介绍多种计量方法，以识别因果关系。

1.2 估计总体均值

问题：如何估计一个随机变量Y的总体均值\(\mu\)？

随机抽样，用样本均值估计总体均值: \(\bar{y} = \frac{ \sum_{i=1}^N y_i }{N}\)。例：掷硬币，掷到正面记1，掷到反面记-1，易知总体均值是0。假设我们不知道总体均值，可以随机抽取30个观测值（掷30次硬币），计算样本均值，作为总体均值的一个估计。

样本均值具有一个良好的性质：样本均值使下面的函数达到最小值:

\[\begin{align} f(m) = \sum_{i=1}^N (y_i-m)^2 \tag{1.1} \end{align}\]

假设随机抽取了3个观测值：\(y_1\)，\(y_2\)，\(y_3\)，如图1.3所示：

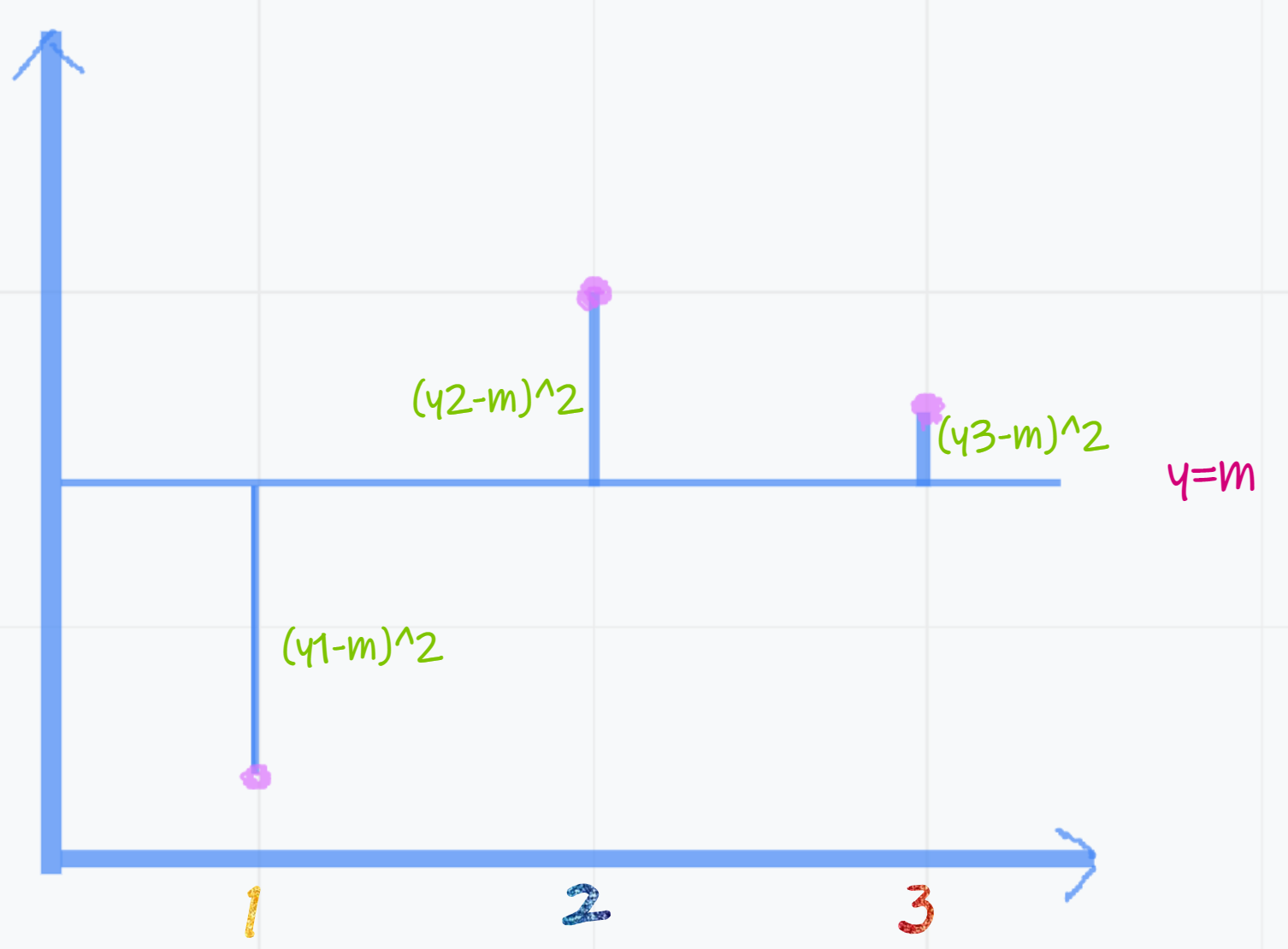
通过随机抽样估计总体均值

图 1.3: 通过随机抽样估计总体均值

纵轴就表示观测值大小；横轴1表示第一个观测值，以此类推。给定一个数m，可以画出水平线，将图中最左边垂线的平方定义为m到第一个观测值（点）的距离，即\((y_1-m)^2\)。类似地，m到第2和3个观测值的距离分别为\((y_2-m)^2\)和\((y_3-m)^2\)。三者相加，就是\(f(m)\)，反映数m（水平线）到这三个观测值（点）的总距离。不同的m，到这些观测值的总距离不一样。m取什么值时总距离最小？答案就是样本均值（请自行证明）。

样本均值是一个随机变量：今天随机掷30次硬币，计算得出一个样本均值。明天再掷30次硬币，也计算出一个样本均值。如此下去10000天。往往各天的样本均值不一样，亦有别于总体均值。

样本均值作为一个随机变量具有统计性质：有期望，也有方差。\(E[ \bar{y} ] = \mu\)。虽然往往各天的样本均值不同，但如果对这10000个样本均值给求平均，那么它大概等于总体均值。平均而言，估计是准确的（简单来说，期望就是平均的意思）。

Y的方差多大？假设\(Y\sim N(\mu,1)\),\(Var[\bar{y}]=\frac{1}{N}\),\(\bar{y}\sim N(\mu,\frac{1}{N})\)。

给定其分布，可以构建置信区间：

\[\begin{align} Prob\left( \lvert \frac{ \bar{y}-\mu }{ 1 / \sqrt{N} } \rvert \leq 1.96\right) = 0.95 \Rightarrow Prob\left( \bar{y} - \frac{1.96}{\sqrt{N}} \leq \mu \leq \bar{y} + \frac{1.96}{\sqrt{N}} \right) = 0.95 \tag{1.2} \end{align}\]

基于置信区间，可做假设检验。原假设\(H_0:\mu=0\)。如果置信区间包含0，那么我们不能拒绝原假设；否则，我们就要拒绝原假设。（以上数学公式如不明白，请翻阅前置课程统计学、概率论与数理统计的相关内容）

还是同样一个过程，换一个顺序说明，分为5个步骤：

  • 第一步, 建立（计量）模型：\(\epsilon_{(i)}=Y_{(i)}-\mu\)。\(\epsilon_i\)表示抽到的第i个值对总体均值的偏离。为了简便，在不引起混淆的时候把下标i省略掉。Y是一个随机变量, \(\mu\)是一个确定值，尽管未知待估。因此，\(\epsilon\)是一个随机变量，E[\(\epsilon\)]=0。模型转换：Y=\(\mu\)+\(\epsilon\),E(\(\epsilon\))=0。这就是Y的统计模型，或者叫计量模型。
  • 第二步，随机抽样。有了计量模型我们需要数据。假设抽到N个观测值。
  • 第三步, 估计总体参数\(\mu\)：\(Min_m f(m) = \sum_{i=1}^N (y_i -m)^2 \Rightarrow m^*=\bar{y}\)。直观的理解：进行随机抽样，抽到多个观测值。这些观测观测值应该围绕着总体均值上下波动。有时抽到的观测值比总体均值大，而有时抽到的观测值比总体均值小。观测数很多时，大于总体均值和小于总体均值的个数大致相当。反过来说，总体均值处于抽到的观测值的中间，总的来说离观测值近。因此，一个自然的想法是，选择距观测值最近的数作为总体均值的估计。上式最小化平方和，因此称称作最小二乘法。由数学推导得，样本均值是总体均值的一个估计量。
  • 第四步, 推导估计量的期望和方差, 公式已在上面给出。
  • 第五步, 构建置信区间, 进行假设检验。

这5步其实就是计量经济学里面最核心的5步。后续的计量分析基本照此展开。

1.3 计量经济学的性质与经济数据

见伍德里奇（2015）《计量经济学导论：现代观点》第五版第1章。

1.4 数学知识复习

见斯托克和沃森（2012）《计量经济学》第二版第2章如下内容：

  • 2.1 随机变量与概率分布
  • 2.2 期望值、均值与方差
  • 2.3 二维随机变量。Q：用数学形式表述：平均而言，受教育程度为本科的人的IQ高于受教育程度为高中的人的IQ？
  • 2.5 随机抽样和样本均值的分布
  • 2.6.1 大数定理和一致性

参考文献