第 2 章 二元线性回归
2.1 二元线性回归模型的定义
二元线性回归模型具有如下的形式:
\[\begin{align} y_i=\beta_0+\beta_1x_i+u \tag{2.1} \end{align}\]
- i表示观测值;
- y:dependent variable, explained variable, response variable;
- x:independent variables, explanatory variables, regressors;
- u:error term, disturbance, unobservables;
- \(\beta_0\):intercept;
- \(\beta_1\):slope parameters。
我们是y、x和u为随机变量。
在不引起混淆的时候,也可略去下标,将模型写作\(y=\beta_0+\beta_1x+u\)。
系数的含义:若\(\bigtriangleup u=0\)(所有其他因素保持不变)时,\(\bigtriangleup y=\beta_1\bigtriangleup x\)(自变量增加1单位,因变量变化多少?)。故\(\beta_1\)其反映x对y的因果影响。
例:教育回报率众所关心。考虑如下的计量模型:
\[\begin{align} wage=\beta_0+\beta_1educ+u \tag{2.2} \end{align}\]
其中,u包括Labor force experience、tenure with current employer、work ethic和intelligence等。\(\beta_1\)度量的是,保持所有其他因素不变,受教育年限增加1年导致的小时工资的变化,反映教育回报率。
“线性”指关于参数是线性的。
2.2 普通最小二乘法的推导
最小二乘(OLS)法的直观理解
假设总体模型为(2.1),从中随机抽取N个观测值,记为{\(((x_i,y_i):i=1,...,N)\)}。绘制散点图,即为图2.1。
问题:基于这些数据,如何估计总体参数?之前,我们估计的总体参数只有总体均值一个;这里,有两个待估计的总体参数:\(\beta_0\)和\(\beta_1\)。怎么估计\(\beta_0\)和\(\beta_1\)?
记\(\beta_0\)的估计量为\(\hat{\beta_0}\),\(\beta_1\)的估计量记为\(\hat{\beta_1}\)。如果确定了\(\hat{\beta_0}\)和\(\hat{\beta_1}\),就可以确定一条直线:\(y=\hat{\beta_0}+\hat{\beta_1}x\)。\(\hat{\beta_0}\)和\(\hat{\beta_1}\)变化,直线也跟着变化。反过来,直线确定了,\(\hat{\beta_0}\)和\(\hat{\beta_1}\)也确定了。即:\({\hat{\beta_0},\hat{\beta_1}}\)与直线是一一对应的关系。那么,确定\(\hat{\beta_0}\)和\(\hat{\beta_1}\),等价于找直线为\(y=\hat{\beta_0}+\hat{\beta_1}x\)。
问题:直线有无限条,需要我们找出其中一条,它在某种意义上是最优的。直观上,该怎么去找?
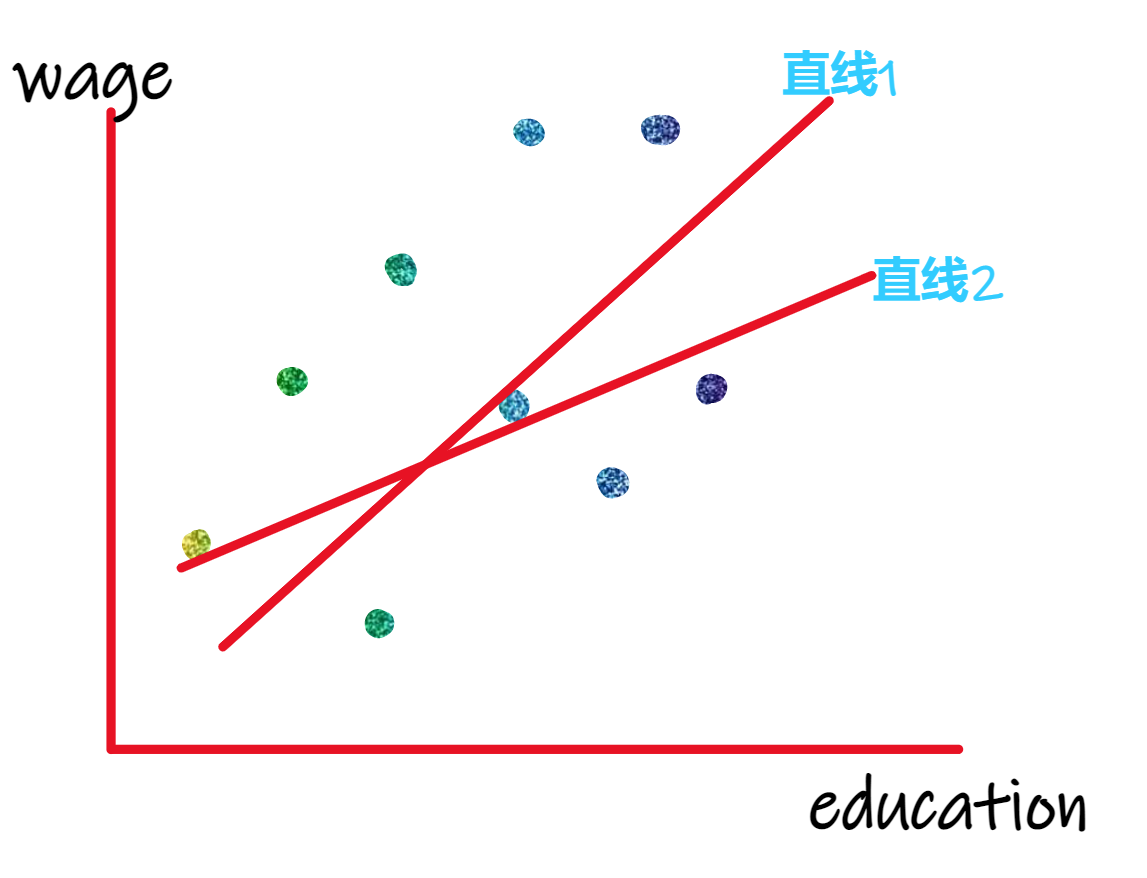
图 2.1: wage and education
回忆:估计总体均值时,我们选择距观测值m(对应观测点)最近的数(对应一条水平线y=m),或者说选择距观测点最近的水平线。
类比:找一条离观测点最近的直线。这里不必是一条水平线,可以是任意走向的直线。
严格地,定义一条给定的直线到各观测点的距离。一种(不是唯一的)定义距离的方法:如图2.2,三个观测点\((x_1,y_1),(x_2,y_2),(x_3,y_3)\),一条给定的直线\(y =\hat{\beta_0}+\hat{\beta_1}x\),做一条从点1出发的垂线,至该直线而止,定义该线段的平方为点1到该直线的距离。数学表达:\((y_1- \hat{\beta_0}-\hat{\beta_1}x_1)^2\)。注意,\(y_1-\hat{\beta_0}-\hat{\beta_1}x\)可能为负,求其平方,保证得到一个正数。类似可求其他点到该直线的距离。总距离为:
\[\begin{align} (y_1 - \hat{\beta_0} - \hat{\beta_1}x_1)^2 + (y_2 - \hat{\beta_0} - \hat{\beta_1}x_2)^2 +(y_3 - \hat{\beta_0} - \hat{\beta_1}x_3)^2 \tag{2.3} \end{align}\]
选择直线与观测点的总距离最小,或者说选择\(\hat{\beta_0}\)和\(\hat{\beta_1}\)使得总距离最小:
\[\begin{align} Min_{\hat{\beta_0},\hat{\beta_1}} (y_1 - \hat{\beta_0} - \hat{\beta_1}x_1)^2 +(y_3 - \hat{\beta_0} - \hat{\beta_1}x_2)^2 + (y_2 - \hat{\beta_0} - \hat{\beta_1}x_3)^2 \tag{2.4} \end{align}\]
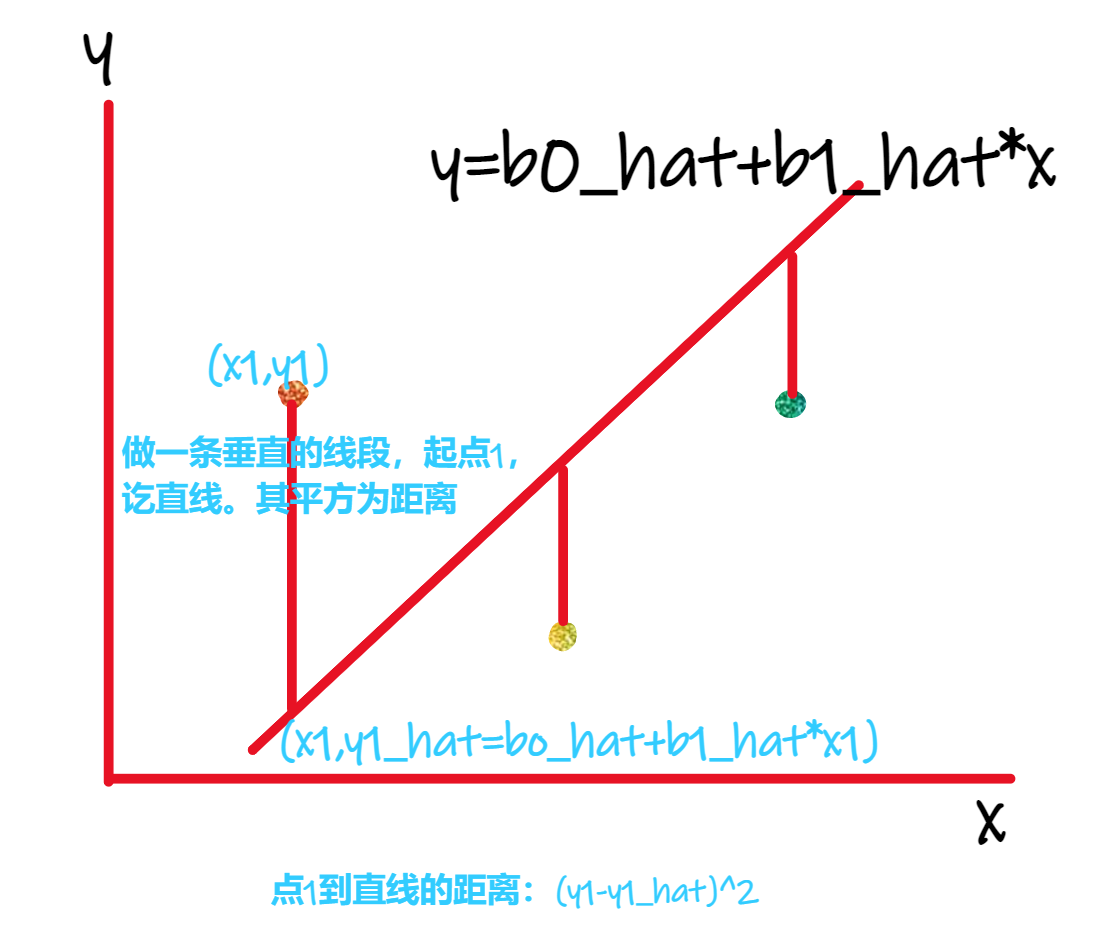
图 2.2: Illustration of the OLS method
定义:
\[\begin{align} \hat{y} \equiv \hat{\beta_0} + \hat{\beta_1}x \\ \hat{u} \equiv y - \hat{y} = y - \hat{\beta_0} - \hat{\beta_1}x \tag{2.5} \end{align}\]
\(\hat{y}\)就是直线的纵坐标,称为拟合值。\(\hat{u}\)是图2.2 中线段,在直线上方记为正,在直线下方记为负,称为残差。可以把最小化问题表述为:
\[\begin{align} Min_{\hat{\beta_0},\hat{\beta_1}} (y_1 - \hat{y_1})^2 +(y_2 - \hat{y_2})^2 + (y_3 - \hat{y_3})^2 = \hat{u_1}^2 +\hat{u_2}^2 + \hat{u_3}^2 \tag{2.6} \end{align}\]
OLS估计量的推导
一般地,有N个观测值,优化问题为:
\[\begin{align} Min_{\hat{\beta_0},\hat{\beta_1}} \sum_{i=1}^N (y_i - \hat{\beta_0} - \hat{\beta_1}x_i)^2 \tag{2.7} \end{align}\]
对择\(\hat{\beta_0}\)和\(\hat{\beta_1}\)求偏导,得到一阶条件:
\[\begin{align} \sum_{i=1}^N (y_i - \hat{\beta_0} - \hat{\beta_1}x_i) = 0 \\ \sum_{i=1}^N (y_i - \hat{\beta_0} - \hat{\beta_1}x_i) x_i = 0 \tag{2.8} \end{align}\]
可以推出:
\[\begin{align} \hat{\beta_1} = \frac{\sum_{i=1}^N (x_i-\overline{x})(y_i-\overline{y})}{(x_i-\overline{x})^2} \\ \hat{\beta_0} = \overline{y} - \hat{\beta_1}\overline{x} \tag{2.9} \end{align}\]
推导见伍德里奇(2015)《计量经济学导论:现代观点》第五版式(2.16)-(2.19)。
\(\hat{\beta_1}\)和\(\hat{\beta_1}\)的计算公式已经给出来了。两个估计量均是观测值{\(((x_i,y_i):i=1,...,N)\)}的函数。由于我们把x和y视作随机变量,随机变量的函数依然是随机变量。
程序模拟
写了一个Fortran小程序。它从总体中随机抽取一个样本,包含30个观测值,每个观测值包含x和y两个取值(可以将y理解成wage,x理解成education)。
一次随机抽样的结果如图2.3。抽到的第一个观测值的y是0.4187,x是0.1616。第二个观测值的y是0.2976,x是1.3366。因为是随机抽样,第二个观测值y和x的取值不同于第一个观测值的y和x的取值。其他观测值取值如图。基于这些观测值,计算了\(\hat{\beta_1}\),计算结果和详细的计算过程如图2.3。
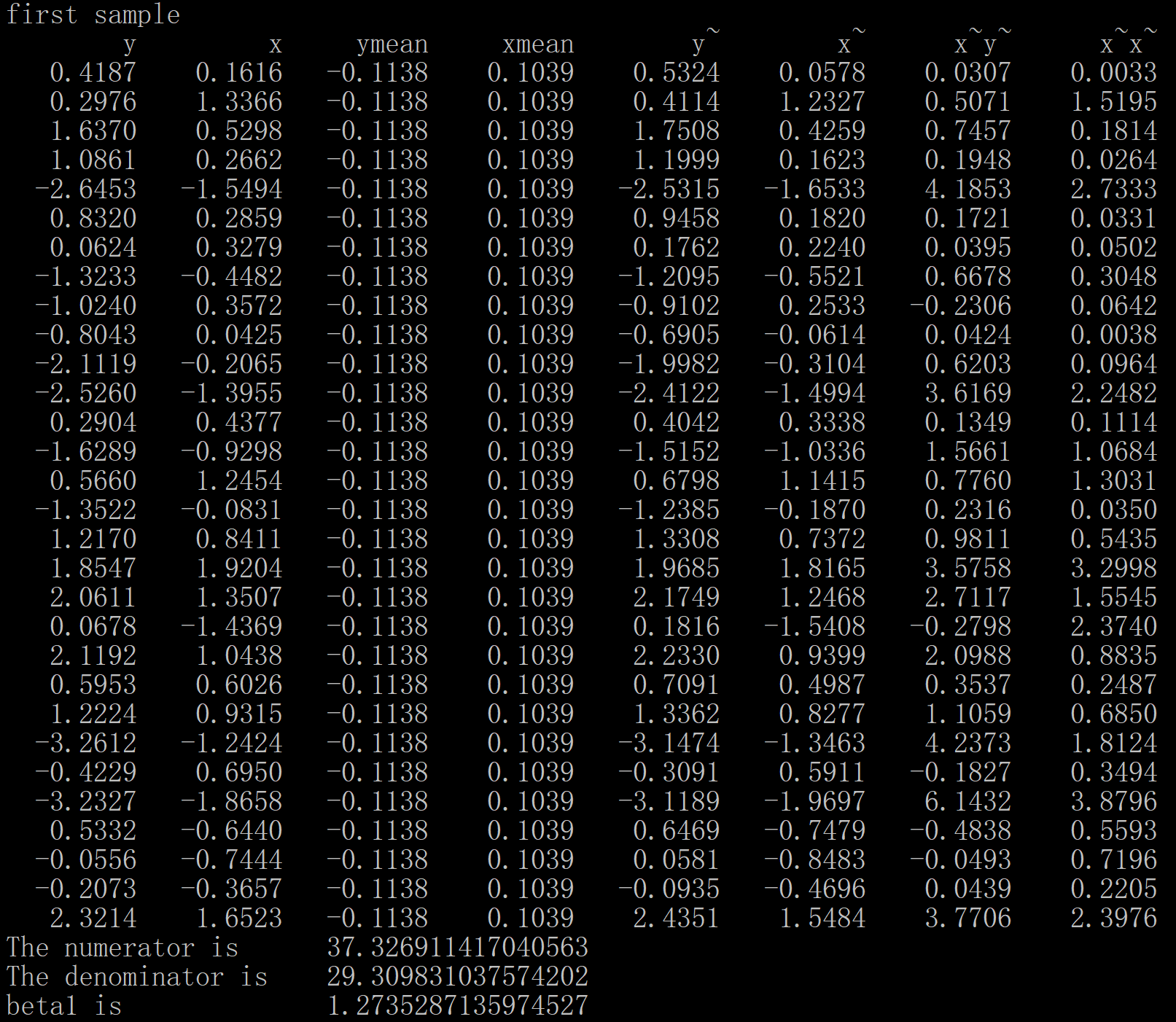
图 2.3: Calculation based on a random sample
把这个过程重复500遍,即进行500次抽样。在每一次抽样中,都随机抽取30个观测值,基于这些观测值重新计算\(\hat{\beta_1}\)。
为便于理解,列出前两次抽样的观测值:图2.4左边是第一次抽样的观测值,右边是第二次抽样的观测值。左右两边的观测值不一样,因是随机抽取的。既如此,基于各样本计算的\(\hat{\beta_1}\)也就不一样。
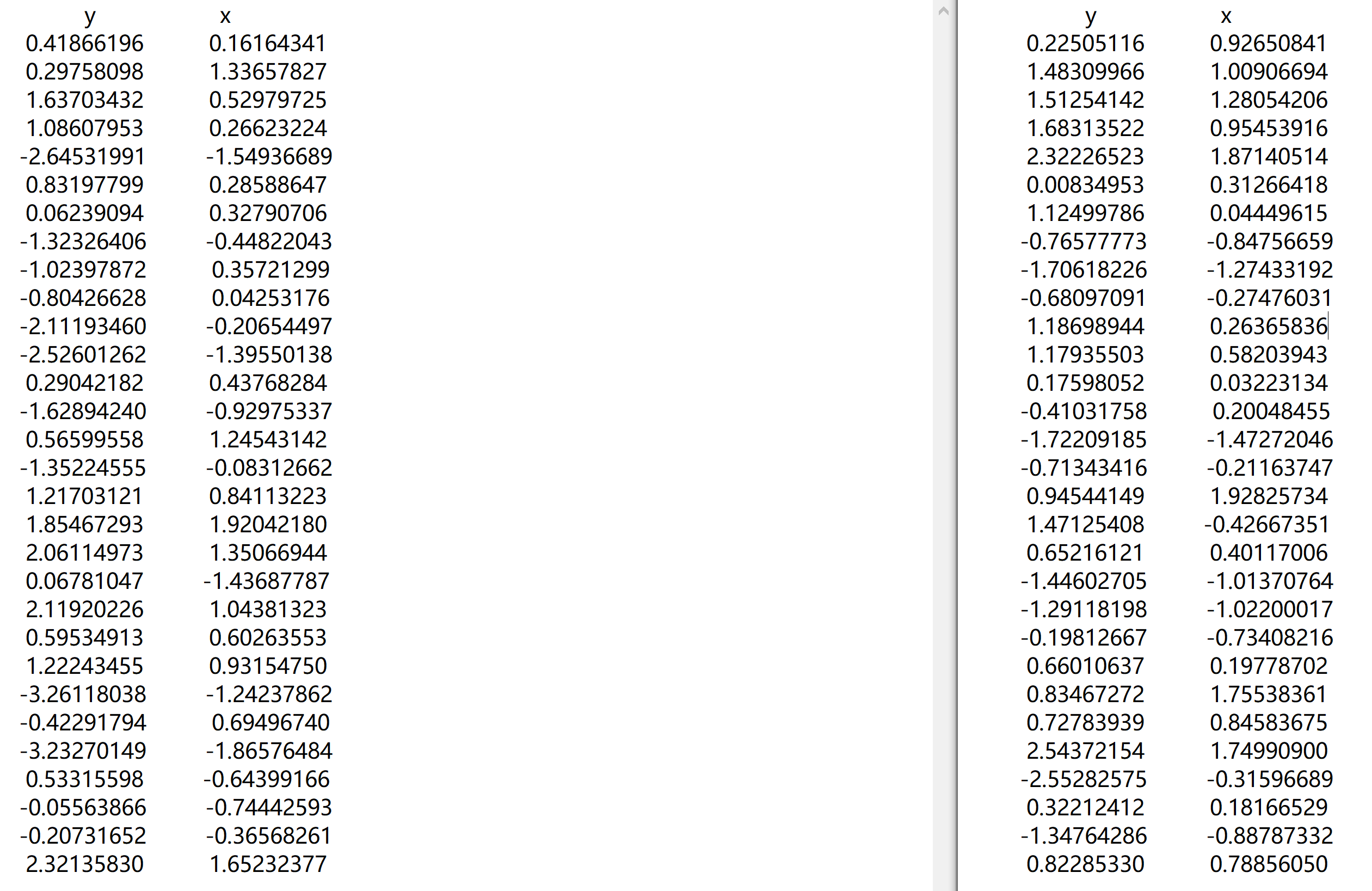
图 2.4: Two random samples
图2.5列出了由500次抽样计算出来的500个\(\hat{\beta_1}\)(图为局部图)。图中第一列表示抽样次数,第二列表示\(\hat{\beta_1}\)。可以看到,各次抽样的\(\hat{\beta_1}\)均不一样,这就是为什么我们说\(\hat{\beta_1}\)是一个随机变量。
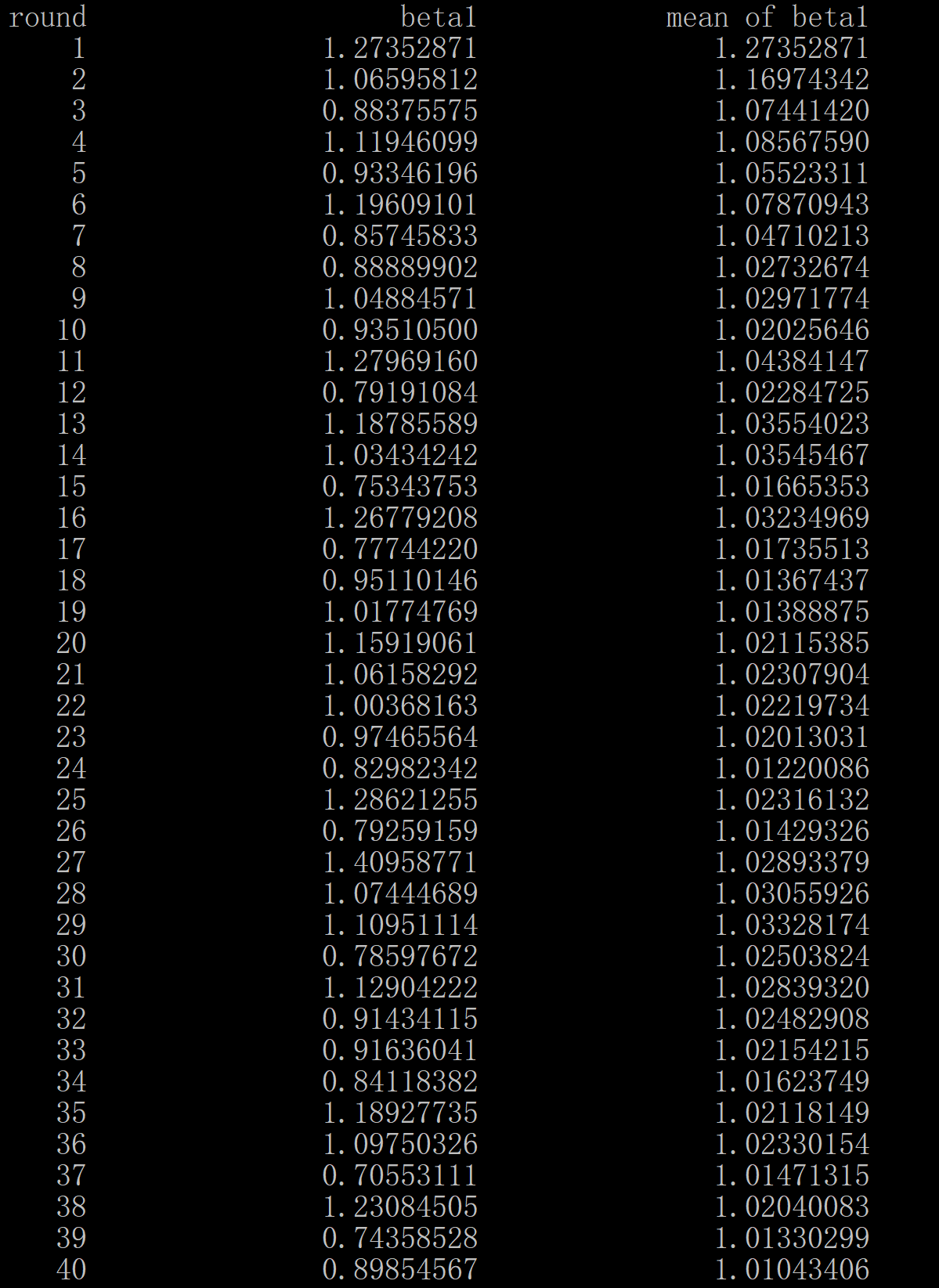
图 2.5: 500 estimates (only first 40 estimates displayed)
总结:因为x和y是随机的,每次抽样得到的x和y不一样,基于这些x和y计算出来的\(\hat{\beta_1}\)不一样,故\(\hat{\beta_1}\)是一个随机变量。
估计教育回报率
伍德里奇(2015)《计量经济学导论:现代观点》第五版例2.4基于数据“WAGE1.dta”估计了计量模型:\(wage=\beta_0+\beta_1educ+u\)。结果显示,\(\hat{\beta_0}=-0.90,\hat{\beta_1}=0.54\)。\(\hat{\beta_1}\)的含义:in the sample, one more year of education was associated with an increase in hourly wage by 0.54 dollar。注意,这里没有其他条件不变这个限定条件。一般而言,\(\hat{\beta_1}\)和\(\beta_1\)的含义是不一样的。
一阶条件的含义
一阶条件也可写成:
\[\begin{align} \sum_{i=1}^N \hat{u_i} = 0 \\ \sum_{i=1}^N \hat{u_i}x_i = 0 \tag{2.10} \end{align}\]
含义:(1)正负偏离相抵;(2)残差与自变量不相关。Q:为什么?[提示:想想相关系数的公式]。
一阶条件的直观展示如图2.6。仍然使用伍德里奇(2015)《计量经济学导论:现代观点》第五版例2.4的数据,绘制散点图,\(\hat{u_i}\)作为纵轴,education作为横轴。
首先看第一个一阶条件:残差有正的也有负的,图2.6中正负偏差相抵。再看第二个一阶条件。图2.6中\(\hat{u_i}\)和education之间没有明显的正的线性关系的或负的线性关系,二者的相关系数为0。
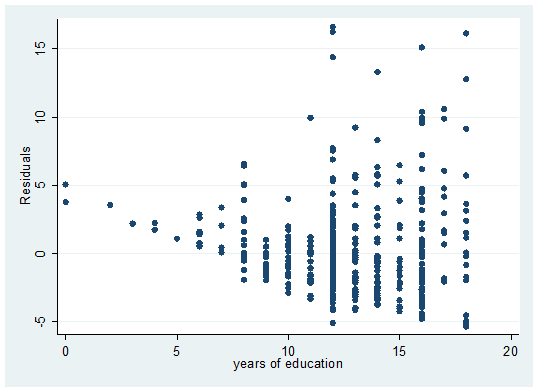
图 2.6: Calculation based on a random sample
拟合优度
见伍德里奇(2015)《计量经济学导论:现代观点》第五版第35-37页。
2.3 OLS估计量的期望和方差
问题:反过来用educ对wage做回归,可不可以?有没有意义?
数学上没有问题。Stata演示结果略。经济学上没有意义。一般的结论:用变量1对变量2回归,不能保证变量2的估计系数有意义。
为了使估计系数有意义,需要施加约束。什么是有意义?通常,满足下式,称有意义:
\[\begin{align} E[\hat{\beta_1}] = \beta_1 \tag{2.11} \end{align}\]
含义:\(\hat{\beta_1}\)是一个随机变量。我们不能保证每一次抽样得到的\(\hat{\beta_1}\)都等于\(\beta_1\);通常前者不等于后者。我们希望至少保证当把这个事情重复很多遍,比如说我们刚才抽样500次,得到的500个\(\hat{\beta_1}\)的平均值等于\(\beta_1\)。或者说,上式成立。期望表示的就是“平均而言”。上式是说,平均而言,\(\hat{\beta_1}\)反映/识别了因果关系。
问题:施加什么条件才能使上式成立?
直接思考这个问题有一定难度。可以从考虑一个简单的问题开始。如果E[IQ|受教育程度=本科]>E[IQ|受教育程度=高中](受教育程度等于本科的人的IQ平均来说大于受教育程度等于高中的人的IQ),那么E[收入|受教育程度=本科]-E[收入|受教育程度=高中](本科生的收入的均值减去高中生的收入的均值)是否反映受教育程度和收入之间的因果关系?即该差值是否完全由受教育程度的差异所致?如果不能的话,将这一前提条件替换成什么条件可使这一差分反映因果关系?
考虑第一小问:本科生平均收入比高中生平均收入高,既因接受了更多的教育,又因本科生IQ平均来说比高中生高。故给定该前提条件,该差值不能反映受教育程度和收入之间的因果关系。
考虑第二小问:换成E[IQ|受教育程度=本科]=E[IQ|受教育程度=高中]。我们之前担心存在遗漏变量问题:本科生和高中生的IQ不相同,因此,不知道收入差异到底是受教育程度不同还是IQ不同所致。改成这一前提条件,回避了这一问题。
即使如此,本科生和高中生在别的方面存在差异。如,一般来说,家庭收入越高,对小孩的教育投入越多,小孩上大学的概率越高。又如,本科生和高中生的道德品质可能有差异。等等。为此,按照上面的逻辑,我们还需要增加如下的前提条件:
\[\begin{align} E[家庭收入|受教育程度=本科]=E[家庭收入|受教育程度=高中] \\ E[道德品质|受教育程度=本科]=E[道德品质|受教育程度=高中] \\ ... \tag{2.12} \end{align}\]
问题在于,可以列出成百上千个前提条件,因为影响收入的因素众多。思考:可不可以化繁为简,用一个简单的式子概括一系列前提条件?这个简单的式子是什么?
下式符合要求:
\[\begin{align} E[u|受教育程度=本科]=E[u|受教育程度=高中] \tag{2.13} \end{align}\]
干扰项的定义就是除了我们纳入模型的因素以外,未纳入模型的因素的综合影响。数学上,可以将u写成IQ、家庭收入、道德品质等一众未纳入模型的因素的函数。上式表示,本科生和高中生除受教育程度以外各因素的综合影响平均而言相等,或者说给定受教育程度,受教育程度以外各因素的综合影响的期望为一个常数。
在这个前提条件满足的情况下,E[收入|受教育程度=本科]-[收入|受教育程度=高中]能够反映受教育程度和收入之间的因果关系。注意这只是一个假设,成不成立是另外一回事。这里只是说如果假设成立,那么我们可以继续进行数学推导。
一般地,受教育程度可以取多个值,如小学、初中、高中、本科、研究生等。将前提条件换成:
\[\begin{align} E[u|educ] = Constant \tag{2.14} \end{align}\]
表示,不管受教育程度取何值,除受教育程度以外各因素的综合影响平均而言均相等。
这是保证OLS估计量有意义的核心假设。此外,我们还需要其他一些假设。
三个假设
(1)假设1(随机抽样):我们有一个服从总体模型(2.1)的随机样本;
(2)假设2(样本中解释变量有波动):样本中x取不尽相同的值。如不然,则无法研究x变化如何影响y;
(3)假设3(零条件均值):\(E[u|x]=0\)。零条件均值假设与前述条件均值为常数本质上是一回事(想想为什么)。零条件均值假设的含义:x变化时,所有其他因素对y的综合影响平均意义上保持不变。。或者说,x对于预测其他因素对y的综合影响的均值无帮助。在教育回报率的例子中,这意味着,不管受教育程度怎么变化,所有其他因素对收入的综合影响平均意义上保持不变(合理吗?)
零条件均值假设是假设,未必是事实。如果它成立,我们可以在它基础上进行推导。但我们需要检查它在现实中是否成立。
OLS估计量的无偏性
若计量模型(2.1)满足假设1-3,可推出:\(E[\hat{\beta_0}]=\beta_0,\ E[\hat{\beta_1}]=\beta_1\),称OLS估计量是无偏的。证明见伍德里奇(2015)《计量经济学导论:现代观点》第五版第2.5节定理2.1。
程序模拟(续)
接2.2中的程序模拟。疑问:500次抽样怎么抽的?这里予以明确。假设真实的模型为:
\[\begin{align} y=x+u, x\ and\ u \sim N(0,1), x\ and\ u\ are\ independent. \tag{2.15} \end{align}\]
这里,\(\beta_0=0,\beta_1=1\)。
抽样:以抽取第一个观测值为例,我们从一个标准正态分布里随机抽取一个\(x_1\),从另一个独立的标准正态分布里随机抽取一个\(u_1\),把它们加起来,就得到\(y_1\)。由此得到第一个观测值\((x_1,y_1)\)。如此,我们抽第2至30个观测值,组成一个样本。这是一次抽样。基于这一次抽样,计算一个\(\hat{\beta_1}\)。重复这一过程,进行第2至500次抽样。每次抽样均包含30个观测值,计算得到一个\(\hat{\beta_1}\)。共得到500个\(\hat{\beta_1}\)。
这一过程满足假设1-3,包括\(E(u|x)=0\)。为什么?因此:
\[\begin{align} E[\hat{\beta_1}]=1 \tag{2.16} \end{align}\]
这是理论结果。是否500次抽样的\(\hat{\beta_1}\)的均值约等于1?绘制500个\(\hat{\beta_1}\)的直方图如图2.7。由图,\(\hat{\beta_1}\)不尽相同,有的时候比较小,甚至达到0.3,而有的时候比较大,甚至达到1.7。就是说由一个随机抽取的样本计算的\(\hat{\beta_1}\)可能离总体参数很远。但\(\hat{\beta_1}\)出现在总体参数1附近的频率最大。总体上,\(\hat{\beta_1}\)围绕着1分布,取到极端值的频率小。
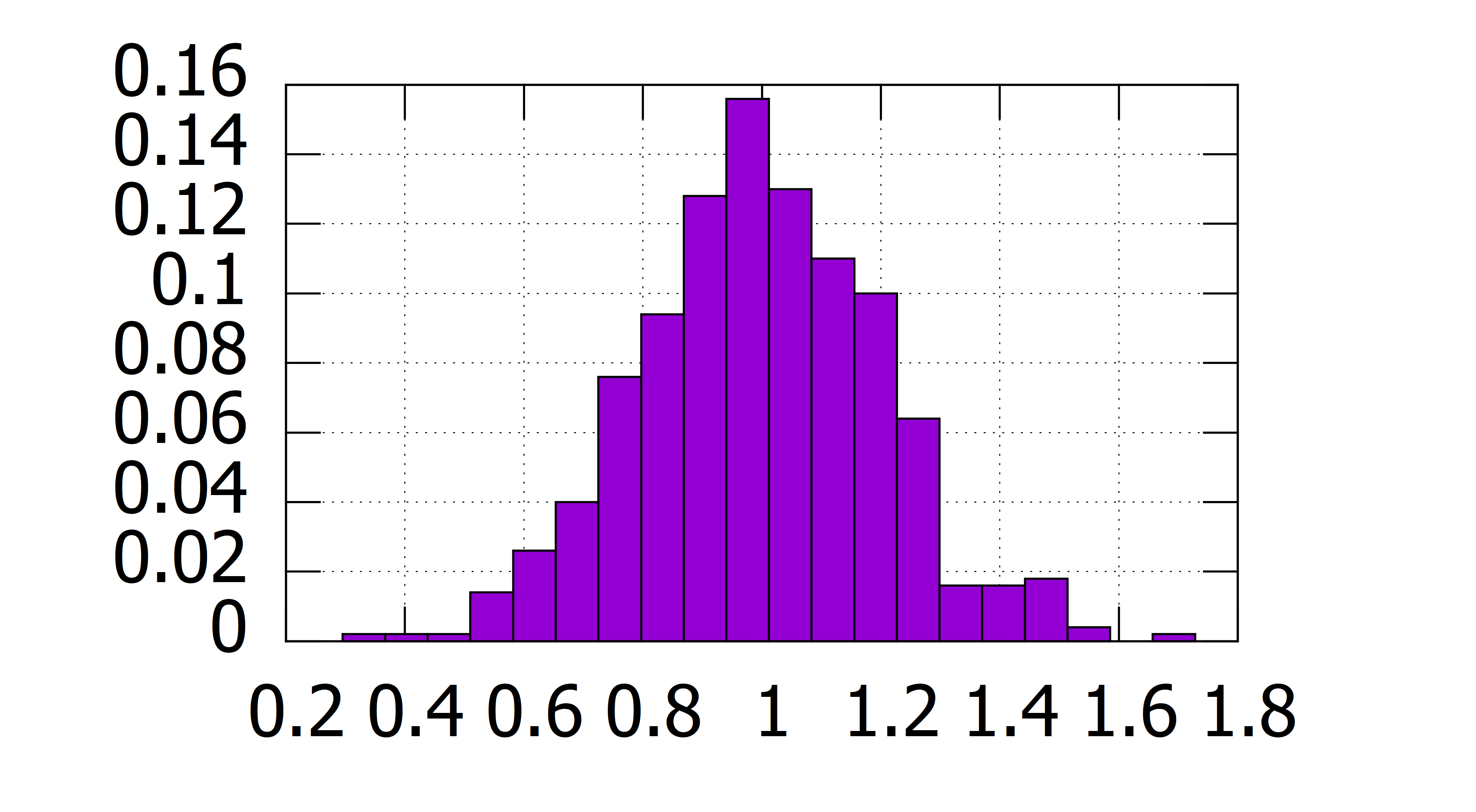
图 2.7: Histogram of 500 estimates
图2.8展示了前若干个\(\hat{\beta_1}\)的均值。如最右端横轴是500,纵轴表示前500次抽样的\(\hat{\beta_1}\)的均值,它约等于1。
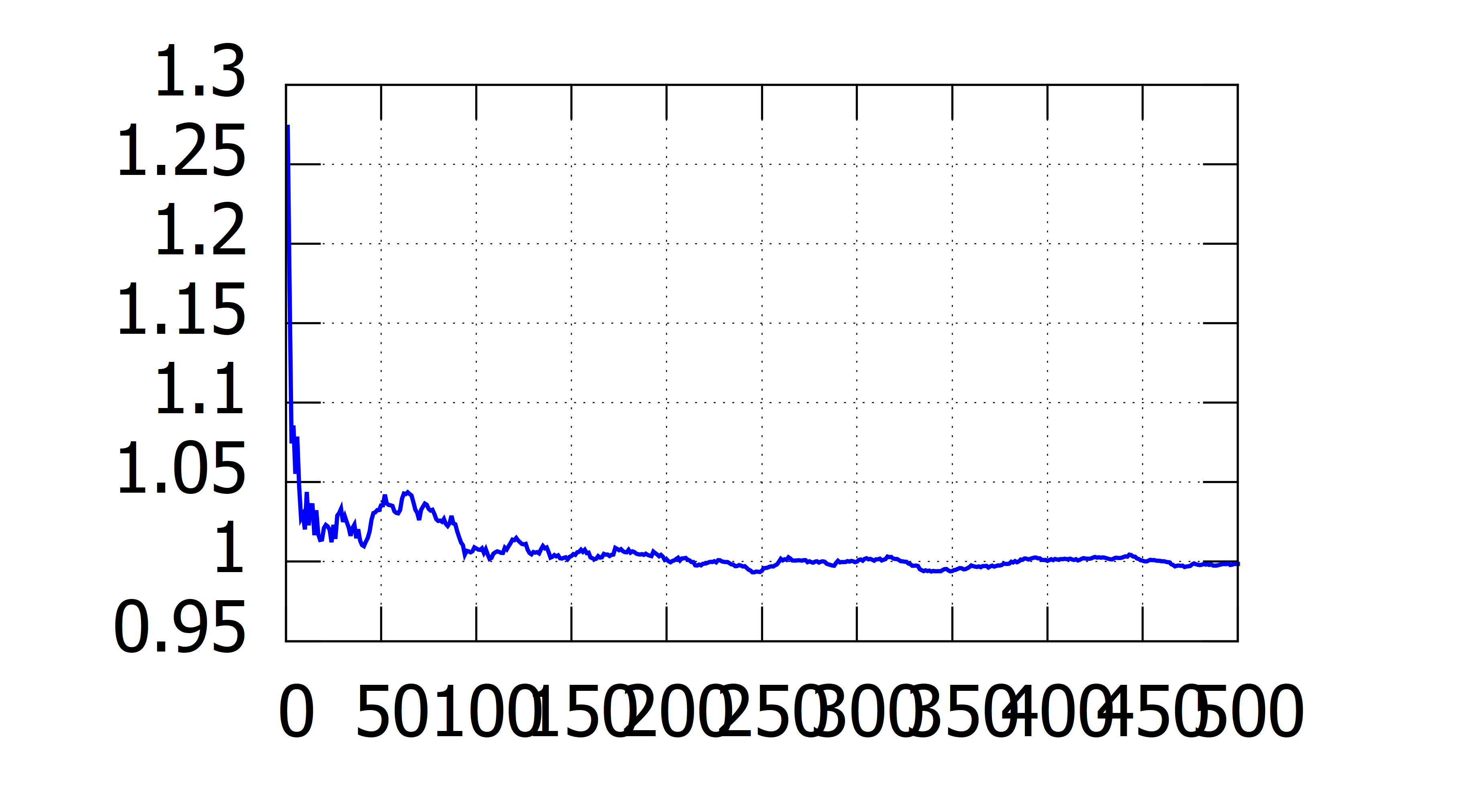
图 2.8: Mean of estimates
这个形象的例子说明在满足假设1-3的情况下,基于一个样本计算的\(\hat{\beta_1}\)通常不等于\(\beta_1\),还可能离\(\beta_1\)比较远,但\(\hat{\beta_1}\)的均值等于\(\beta_1\)。
零条件均值、无偏性与因果关系
我们很多次把最小二乘回归跟因果关系联系在一起。并非牵强附会。
因果关系的定义:x变化时其他因素不变,y怎么变化?反映从x到y的因果关系。
零条件均值假设:x变化的时候,平均而言其他因素不变。零条件均值假设跟因果关系定义的前半句非常相似,唯一的区别是多了一个“平均而言”。社会科学不同于自然科学,一般来说我们没办法进行实验,保持其他因素完全不变。比如,我们抽到若干个本科生和若干个高中生,除了受教育程度不一样,本科生和高中生在别的各方面也不一样。每一个人都是独特的,没有办法保持IQ严格不变,我们尽可能做到保持本科生和高中生的IQ的均值一样。故我们不得不加上“平均而言”,在数学上用期望表示。
如果零条件均值假设成立,可以推出无偏性:平均而言,\(\hat{\beta_1}\)等于\(\beta_1\),即平均而言\(\hat{\beta_1}\)反映因果关系,跟因果关系的定义的后半句非常相似,唯一的区别依然是多了一个“平均而言”。因为零件均值假设中有一个“平均而言”,这里也得有一个。
OLS估计量的方差
见伍德里奇(2015)《计量经济学导论:现代观点》第五版第46-51页。
2.4 函数形式
前已述及,“二元线性回归中”的“线性”指关于参数是线性的。至于自变量,可以是绝对值,也可以取对数。下面两个模型都是二元线性回归模型:
- 收入和受教育程度的另一个计量模型:\(log(wage)=\beta_0+\beta_1educ+u\);
- CEO薪水和公司销售额的一个计量模型:\(log(salary)=\beta_0+\beta_1log(sales)+u\)。
Q:以上两个模型中系数\(\beta_1\)作何解释?例如,第一个模型中,\(\beta_1=0.05\),是什么含义?[如无头绪,请先阅读伍德里奇(2015)《计量经济学导论:现代观点》第五版第38-41页,再回答问题]
2.5 最小二乘法:再考察
最小二乘法到底在干什么?之前我们给出了一种理解(称为理解1):把观测值画在二维图中,找离这些观测值最近的直线。这是一种直观的理解,但不是唯一的理解。下面我们给出另外两种理解。
理解2
\[\begin{align} y_i=\hat{\beta_0}+\hat{\beta_1}x_i+\hat{u_i}=\hat{y_i}+\hat{u_i} \tag{2.17} \end{align}\]
也就是说我可以把y分解成两部分:拟合值\(\hat{y}\)和残差\(\hat{u}\)。这两部分有什么关系?
\(\sum_{i}(\hat{\beta_0}+\hat{\beta_1}x_i)\hat{u_i}=0\)。为什么?[提示:使用一阶条件]。意味着\(\hat{y}\)和\(\hat{u}\)不相关。为什么?[提示:使用相关系数的公式]
直观上,可以绘制\(\hat{u_i}\)和\(\hat{y_i}\)的散点图。仍利用教育回报率的例子,绘制\(\hat{y_i}\)(横轴,怎么计算?)和\(\hat{u_i}\)(纵轴)的散点图如图2.9。可见,两者不存在线性关系,它们的相关系数为0。
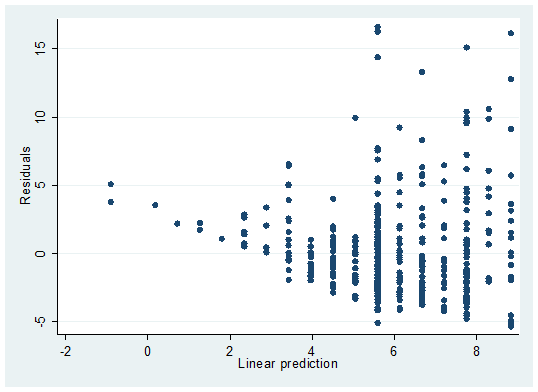
图 2.9: What does OLS method do?
总之,最小二乘法是做分解:将因变量分解成拟合值和残差这两个不相关的项。
理解3
换一个角度,利用线性代数的知识。考虑过原点的回归模型:
\[\begin{align} y=\beta_1x+u \tag{2.18} \end{align}\]
也就是说,\(\beta_0=0\)。
OLS估计量为(推导见伍德里奇(2015)《计量经济学导论:现代观点》第五版第51页):
\[\begin{align} \hat{\beta_1}=\frac{\sum_{i}x_iy_i}{\sum_{i}x_i^2} \tag{2.19} \end{align}\]
有两个观测值:\((x_1=2,y_1=1),(x_2=0,y_2=2)\)。代入上面的公式,得:\(\hat{\beta_1}=0.5\)。
将两个观测值的回归方程用线性代数表示:
\[\begin{align} \left( \begin{array}{c} 1 \\ 2 \end{array} \right) = \left( \begin{array}{c} 2 \\ 0 \end{array} \right) \times0.5 +\left( \begin{array}{c} 0 \\ 2 \end{array} \right) = \left( \begin{array}{c} 1 \\ 0 \end{array} \right) +\left( \begin{array}{c} 0 \\ 2 \end{array} \right) \tag{2.20} \end{align}\]
记向量\(\vec{y}=(1,2)',\vec{x}=(2,0)',\vec{u}=(0,2)'\)。把这些向量画在二维图中:
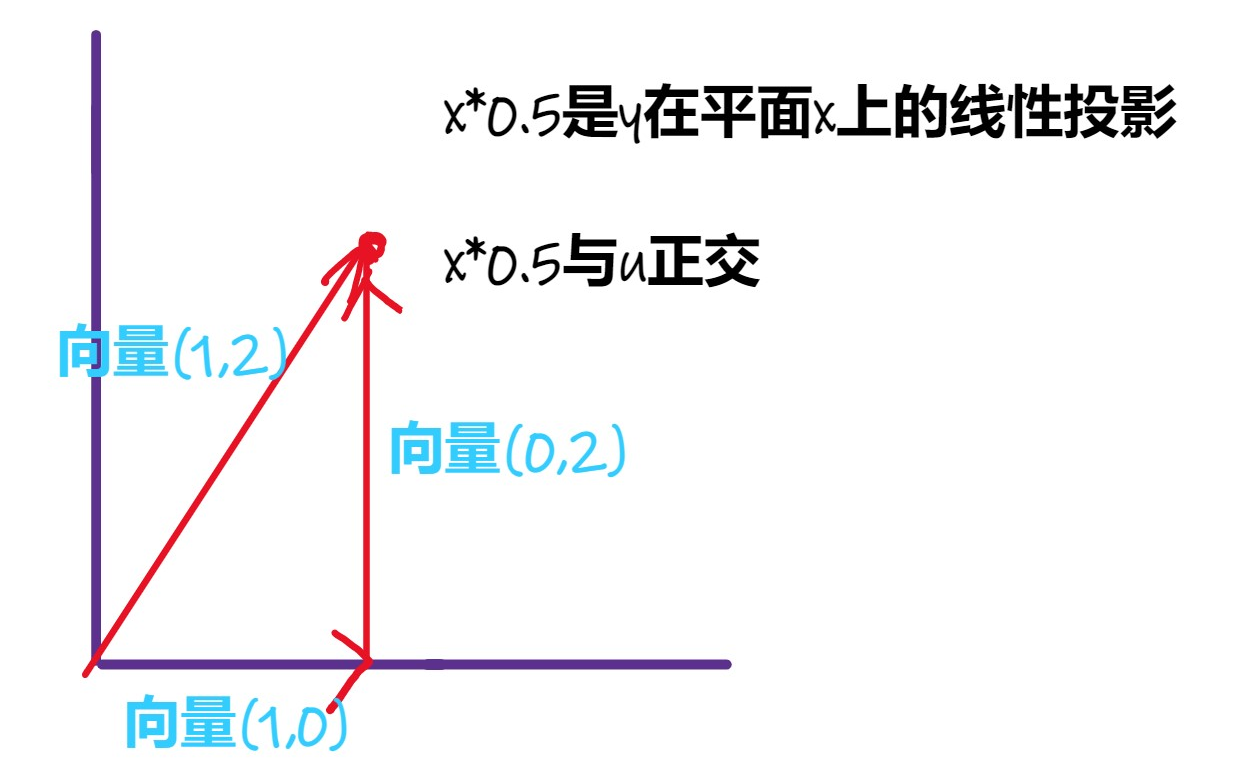
图 2.10: What does OLS method do? (continued)
由图可见,OLS法是做线性投影:将向量\(\vec{y}\)在向量\(\vec{x}\)确定的平面上做线性投影,线性投影为拟合值,投影剩下的部分就是残差。
2.6 零条件均值假设:成立吗?
一个物理学家,一个化学家和一个经济学家落难孤岛,正值饥肠辘辘,海上漂来一盒罐头。物理学家提议用岩石砸开罐头,化学家主张生火加热使其膨胀破裂,此时,经济学家慢条斯理地说:“你们的方法太复杂了,假设有一个开瓶器,我们就可以轻松撬开它。”
资料来源:https://www.douban.com/group/topic/252843954/?_i=7975810BnpGaYU
当零条件假设成立时,OLS估计量无偏,平均而言能够反映因果关系。问题是,什么情况下零条件均值假设成立?
随机实验
如果x是随机分配的,那么零条件均值假设成立。比如,一个农学家研究施肥量(记为x)对作物收成(记为y)的影响。他可以做自然实验:找100块1亩大小的土地,随机分成10组,分别施以0、1、2……、9单位的肥料。某块地获施肥量多寡,纯系运气,与别的信息无关。也就是说,知道该块地的施肥量对于推测该块地的别的信息了无帮助。用数学术语讲: 对于任一施肥量,别的信息对此的条件期望是一个常数,即零条件均值假设成立。
问题在于,在经济学里,很难开展随机实验,原因有二:其一,经济学领域的随机实验的成本可能较高,如为了解基础设施对经济增长的影响,随机实验的思路选择100个村子,随机分成2组,给一组修路,对另一组不做处理。修路成本高昂显而易见。其二,为估计教育回报率,随机实验的思路是随机地给不同小孩不同的受教育程度。但为什么有的小孩就能得到高学历,而有的小孩初中毕业就不得不进入电子厂?这是伦理压力。
检验零条件均值假设是否成立
定理:\(E[u|x]=0=>Cov(x,u)=0,Corr(x,u)=0\)。证明见斯托克和沃森(2012)《计量经济学》第二版第27页。
反过来,如果相关,零条件均值假设不成立。这为我们提供了一个判断零条件均值假设成不成立的思路:一般来说,很难直接判断零条件均值假设是否成立,因其抽象。但容易判断x和u是不是相关的。如果有理由认为x和u相关,则有理由认为零条件均值假设不成立。
例1:\(y=\beta_0+\beta_1educ+u\)。干扰项包含除教育以外其他影响收入的因素,包括IQ。IQ和受教育程度x应是正相关的。而IQ是u的一个组成部分,因此我们有理由认为u和educ也是相关的。进而有理由认为零条件均值假设不成立。这里存在所谓的遗漏变量问题:遗漏掉IQ,它与educ相关。既如此,OLS估计量不满足无偏性,平均而言不能反映因果关系。
例2:\(cons=\beta_0+\beta_1transfer+u\)(消费<-转移支付)。Q:u是哪些因素的综合影响?这些因素各自与transfer相关吗?如果相关, 是正相关还是负相关?0条件均值假设成立吗?
另外一种情况是不仅x会影响y,反过来y也会影响x。
例3:基础设施和经济发展水平的关系。良好的基础设施促进经济发展。反过来,经济发达,政府税收多,基础设施多。也就是说,基础设施和经济发展水平双向影响。
例4:国民总收入和总消费的关系。
如果x和y双向影响,那么x和u相关。证明如下:

图 2.11: reverse causilty and biased estimator
这就是反向因果问题。当其存在的情况下,零条件均值假设不成立,OLS估计量有偏, 平均而言不能反映因果关系。
遗漏变量或反向因果问题在实践中非常常见,以致于很多时候,简单做最小二乘回归没有什么意义。处理遗漏变量或反向因果问题至关重要。如何处理?本讲义后述各种方法,皆旨在处理这两个问题。
参考文献
- 伍德里奇. 计量经济学导论(第五版)[M]. 中国人民大学出版社, 2015.
- 斯托克, 沃森. 计量经济学(第三版)[J]. 格致出版社, 2012.